СТРУКТУРА И ЭНЕРГЕТИЧЕСКИЕ ЗОНЫ ПОЛУПРОВОДНИКОВ

В абсолютном большинстве случаев устройства современной электроники изготавливаются из полупроводниковых материалов. Полупроводниками обычно называют материалы, удельное сопротивление которых больше, чем у проводников (металлов), но меньше, чем у изоляторов (диэлектриков). Сразу следует заметить, что различие между полупроводниками и диэлектриками только количественное, тогда как различие между полупроводниками и металлами более принципиальное - качественное. Полупроводники являются разновидностью диэлектриков, можно сказать, что они являются диэлектриками с уменьшенным удельным сопротивлением, тогда как с металлами у них значительно меньше общего.

Для того чтобы представить особенности полупроводниковых материалов, следует рассмотреть их структуру и энергетические зоны.

Любое твердое тело представляет собой множество атомов, сильно взаимодействующих друг с другом благодаря малым межатомным расстояниям. Эти расстояния минимальны у металлов и максимальны у диэлектриков. Однако в любом случае всю совокупность атомов в куске твердого тела следует рассматривать как единую целую структуру, которая подобно атому характеризуется некоторым единым энергетическим спектром. Особенность этого спектра в том, что он состоит из дискретных разрешенных зон.

Строго говоря, разрешенные зоны сами имеют дискретную структуру и состоят из большого числа разрешенных уровней (равного числу атомов в рассматриваемом образце), неэнергетические расстояния между ними малы (~10^-22эВ), поэтому иногда разрешенные зоны 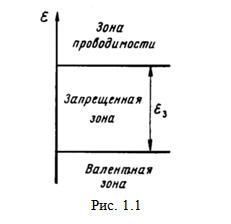можно считать сплошными.

На рис. 1.1 приведена зонная диаграмма для полупроводника. Прежде всего, следует обратить внимание на запрещенную зону (зону запрещенных энергий), которая разделяет разрешенные зоны. Отметим, что у диэлектриков ширина запрещенной зоны больше, чем у полупроводников, а у металлов разрешенные зоны сливаются, так что заращенной зоны у них нет. Ширина запрещенной зоны ε_з, определяющая энергетический промежуток запрещенных энергий, является важнейшим параметром полупроводника. Для наиболее часто используемых в электронике полупроводников германия, кремния и арсенида галлия - ширина запрещенной зоны равна соответственно 0,7; 1,1 и 1,4 эВ.

Верхняя разрешенная зона называется зоной проводимости. Электроны, находящиеся в этой зоне, обладают довольно большой энергией и могут ее изменять под действием электрического поля, перемещаясь в объеме полупроводника. Электропроводность полупроводника и определяется этими электронами.

Нижняя разрешенная зона называется валентной зоной. Энергетические уровни этой зоны обычно заполнены электронами внешней оболочки атомов - внешних устойчивых орбит (валентными электронами). При наличии свободных уровней в валентной зоне электроны также могут изменять свою энергию под действием электрического поля. Если же все уровни зоны заполнены, то валентные электроны не смогут принять участие в проявлении электропроводности полупроводника.

Рассмотрим теперь структуру собственного (беспримесного) полупроводника. Монокристаллические полупроводники представляют собой кристаллы с регулярной структурой. Кристаллическая решетка кремния (германия) называется тетраэдрической или решеткой типа алмаза. Она характерна для всех четырехвалентных элементов. Для определенности будем рассматривать структуру кремния. Это справедливо хотя бы потому, что приблизительно 97% всех изделий полупроводниковой электроники на сегодняшний день выполняются на основе кремния.

Связь атомов в кремнии устанавливается вследствие наличия специфических обменных сил, возникающих при парном объединении валентных электронов. У соседних атомов кремния появляются общие отбиты, на которых в соответствии с фундаментальным положение физики, называемым принципом запрета Паули, находится не более двух электронов. Поскольку атом кремния имеет четыре валентных электрона, то он использует эти электроны для связи с четырьмя другими атомами, которые, в свою очередь, также выделяют по одному валентному электрону для связи с каждым из своих четырех соседних атомов. Таким образом, получается, что любой атом кремния связан с каждым из четырех соседних атомов общей орбитой, причем на этой общей орбите находится два электрона. Такая связь атомов называется парно-электронной или ковалентной.

На рис. 1.2 приведена упрощенная модель решетки (а) и зонная энергетическая диаграмма (б) для беспримесного кремния. На этом рисунке между каждыми двумя атомами кремния проведены две связывающие их прямые линии. Каждая такая линия символизирует собой наличие электрона на общей орбите у этих атомов. Ее принято называть связью (валентной связью).  Валентный электрон, находящийся в такой связи, по энергии расположен в валентной зоне.

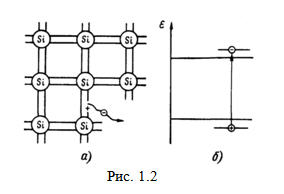Электроны во всех связях будут присутствовать только при температуре абсолютного нуля. По мере нагревания полупроводника происходит нарушение связей, т.е. некоторые валентные электроны получают от тепла энергию, необходимую для их перехода в зону проводимости (рис. 1.2,б). Такой переход соответствует ионизации связи и выходу из нее электрона (рис. 1.2, а). Появившиеся свободные электроны будут принимать участие в образовании тока в полупроводнике (при приложении напряжения к полупроводнику).

Появление вакантных уровней в валентной зоне свидетельствует о том, что для валентных электронов появляется возможность изменять свою энергию (появляется возможность переходить с одного разрешенного уровня валентной зоны да другой), а следовательно, участвовать в процессе протекания тока через полупроводник. С повышением температуры возрастает число свободных электронов в зоне проводимости и число вакантных уровней в валентной зоне. Заметим, что этот процесс будет проходить интенсивнее в полупроводниках с узкой запрещенной зоной.

Вакантный энергетический уровень в валентной зоне и соответственно ионизированную валентную связь принято называть дыркой. Дырка является подвижным носителем положительного заряда, равного по модулю заряду электрона. Перемещение дырки (положительного заряда) соответствует встречному перемещению валентного электрона (из связи в связь). Движение дырки есть поочередная ионизация валентных связей.

Отметим, что процесс образования свободного электрона и дырки принято называть генерацией. Поскольку в рассматриваемом случае генерация происходит под действием тепла, то ее можно назвать термогенерацией.

Появление электрона в зоне проводимости и дырки в валентной зоне на энергетической диаграмме (см. рис. 1.2, б) представлено в виде кружочков с соответствующими знаками зарядов. Стрелкой обозначен переход электрона из валентной зоны в зону проводимости.

Таким образом, за счет термогенерации в собственном (беспримесном) полупроводнике, который принято обозначать буквой i, образуются два типа подвижных носителей заряда: свободные электроны n и дырки p, причем их число одинаково (n_i = p_i). Эти носители заряда иногда называют собственными, а электропроводность, ими обусловленную, - собственной электропроводностью. В полупроводниковой электронике, в отличие от собственной электропроводности, наиболее части используют примесную электропроводность, характерную для примесных полупроводников.

ПРИМЕСНЫЕ ПОЛУПРОВОДНИКИ

Примесными полупроводниками принято называть полупроводники, электропроводность которых обусловлена носителями заряда, образующимися при ионизации атомов. Если в кремний ввести атом пятивалентного элемента (например, фосфора), то четыре из пяти валентных электронов этого элемента вступят в связь с четырьмя соседними атомами кремния (подобно атомам собственного полупроводника). Пятый е электрон будет в данном случае избыточным. Он оказывается очень слабо связанным со своим атомом, поэтому оторвать его от атома и превратить в свободный носитель заряда можно даже оторвать его от атома и превратить в свободный носитель заряда можно даже при воздействии малой тепловой энергии.

На энергетической диаграмме, соответствующей рассматриваемому случаю (рис. 1.3), обозначен разрешенный энергетический уровень ε_д, который принес с собой атом фосфора. На этом уровне при очень низкой температуре и будет находиться избыточный электрон фосфора. При незначительном повышении температуры он переходит в зону проводимости и становится свободным. Нейтральный атом фосфора при этом превращается в положительный ион (его заряд обусловлен отсутствием валентного электрона). Количество энергии, необходимое для отделения избыточного электрона и образования иона, называется энергией активации (ионизации) примеси (∆ε_А ≈ 0,1 эВ). Отметим, что ион прочно связан с кристаллической решеткой и не может перемещаться подобно дырке.

Таким образом, появление в кремнии атома фосфора привело к образованию в зоне проводимости свободного электрона. Образование данного электрона не связано с существованием дырки.

 В реальных случаях вводится, конечно, далеко не единственный атом примеси (10¹⁴...10¹⁸ атомов / см³), поэтому и примесных уровней получается довольно много. Примесные уровни образуют примесную зону, которая в рассматриваемом здесь случае будет находиться в запрещенной зоне кремния вблизи зоны проводимости.

Атомы пятивалентной примеси принято называть донорами. Примесные разрешенные уровни, приносимые донорами, называют донорными. Примесные полупроводники, полученные за счет введения доноров, называются электронными, или полупроводниками n-типа. Электропроводность электронных полупроводников определяется свободными электронами, которые здесь являются основными носителями заряда. Дырки в полупроводнике n-типа являются неосновными носителями заряда. Дырок здесь очень мало (n_n ›› р_n), но они все-таки есть (дырки образуются за счет термогенерации подобно собственным носителям в беспримесном полупроводнике).

Итак, за счет введения донорной примеси образуется электронный полупроводник, электропроводность которого определяется электронами, причем число свободных электронов практически равно числу ионизированных доноров.

Рассмотрим теперь дырочный полупроводник или полупроводник р-типа. Такой полупроводник получается за счет введения в него трехвалентных атомов примеси (например, бора). Атомы трехвалентной примеси принято называть акцепторами.

Находясь среди атомов кремния, атом бора образует только три 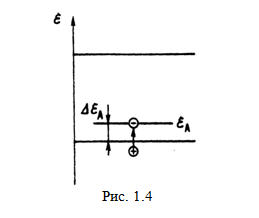заполненные валентные связи. Четвертая связь оказывается незаполненной, однако она не несет заряда, т. е. атом бора является электрически нейтральным. При воздействии даже небольшой тепловой энергии электрон одной из соседних заполненных валентных связей кремния может перейти в эту связь. Во внешней оболочке атома бора появляется лишний электрон, т. е. атом бора превращается в отрицательный ион. Ионизированная связь атома кремния (из которой электрон перешел к атому бора) несет собой уже положительный заряд, являясь дыркой.

На энергетической диаграмме, соответствующей рассматриваемому здесь случаю (рис. 1.4), обозначен разрешенный энергетический (акцепторный) уровень ε_А, который принес с собой атом бора. Этот уровень будет не заполнен лишь при очень низкой температуре. При небольшом повышении температуры один из электронов валентной зоны переходит на акцепторный уровень, затратив при этом небольшую энергию, равную энергии активации примеси (∆ε_А ›› 0,1эВ). Таким образом, получаются дырка (в валентной зоне) и ионизированный акцептор.

Электропроводность дырочного полупроводника определяется дырками, которые здесь являются основными носителями заряда. Электроны в полупроводнике р-типа являются неосновными носителями и их очень мало (р_р ›› n_p).Итак, за счет введения и активации акцепторной примеси образуется дырочный полупроводник, электропроводность которого определяется дырками, причем число и практически равно числу ионизированных акцепторов. При рассмотрении примесных полупроводников обычно используют понятие «концентрация примеси». Концентрацией называется число зарядов или частиц в единичном объеме (например, в 1 см³). Понятно, что чем больше концентрация доноров Nд, тем больше и концентрация электронов, а чем больше концентрация акцепторов N_А, тем больше концентрация дырок в полупроводнике.

Если оба типа примеси находятся в равном количестве (Nд = N_А) принято называть компенсированным. Компенсированный проводник похож на собственный (n_k = p_k), но имеет ряд интересных свойств и отличий.

Необходимо отметить, что рассмотренные выше процессы являются, вообще говоря, обратимыми. Наряду с переходами электронов с нижних энергетических уровней на более высокие происходят и обратные переходы. Особое внимание обратим на то, что одновременно с генерацией пар «электрон-дырка» происходит и обратный процесс - процесс взаимного уничтожения свободного электрона и дырки, который принято называть рекомбинацией (свободный электрон переходит из зоны проводимости в валентную зону). При некоторой установившейся температуре полупроводник находится в состоянии термодинамического равновесия. Процесс генерации уравновешивается процессом рекомбинации.

Одним и основных параметров полупроводника является уровень Ферми, вероятность заполнения которого при температуре, отличной от абсолютного нуля, равна 0,5. Энергетический уровень Ферми представляет собой среднюю термодинамическую энергию тела на один электрон. Фундаментальное положение физики указывает, что уровень Ферми одинаков во всех частях равновесной системы, какой бы разнородной она ни была.

Для собственных полупроводников уровень Ферми проходит по середине запрещенной зоны. В электронном полупроводнике в сравнении с собственным имеется большое число электронов в зоне проводимости, т.е. средняя энергия электронов (и всего полупроводника) здесь будет выше. Следовательно, в электронном полупроводнике уровень Ферми должен находиться выше середины запрещенной зоны, причем, чем больше концентрация доноров, тем выше будет располагаться уровень Ферми. Аналогично можно заключить, что в дырочном полупроводнике уровень Ферми должен быть ниже середины запрещенной зоны, причем тем ниже, чем больше концентрация акцепторов.

Необходимо отметить, что помимо рассмотренных здесь примесных полупроводников в электронике находят применение и так называемые вырожденные полупроводники. У таких полупроводников уровень Ферми обычно располагается в разрешенных зонах: в озоне проводимости для электронного и в валентной зоне для дырочного полупроводника. На практике обычно используются вырожденные полупроводники с сильной степенью вырождения (например, в туннельных диодах), получаемые за счет значительного повышения концентрации примеси (10¹⁹ ...10²¹см ^-3).

 

ОСНОВНЫЕ ПАРАМЕТРЫ ПОЛУПРОВОДНИКОВ

Выше были ниже рассмотрены некоторые параметры полупроводников, в то числе и самый важный - ширина запрещенной зоны. В этом разделе остановимся на параметрах, в той или иной степени влияющих на электропроводность полупроводника. Эти параметры часто используются при описании принципа действия и характеристик многих элементов полупроводниковой электроники.

Вторым по значимости параметром полупроводника (после ε_з), пожалуй, является подвижность носителей заряда μ. Подвижность носителей по определению есть их средняя направленная скорость в полупроводнике при напряженности электрического поля Е = 1 В / см.

Как правило, подвижность электронов μ_n всегда больше подвижности дырок μ_р. Это объясняется большей инерционностью дырок (соответствующей инерционности валентного электрона), чем свободного электрона. Наиболее значительно это проявляется у арсенида галлия. Чем больше подвижность, тем больше скорость движения носителей и тем выше быстродействие полупроводникового элемента. Отсюда становится понятным преимущество высокочастотных элементов, изготовленных из электронного арсенида галлия.

Подвижность носителей заряда зависит от ряда факторов, важнейшим из которых является температура. Зависимость μ от температуры определяется механизмом рассеяния носителей. Поскольку с повышением температуры увеличивается интенсивность колебания атомов кристаллической решетки, то возрастает и число столкновений в единицу времени, следовательно, наблюдается падение подвижности носителей.

Для кремния п-типа можно записать

μ = μ0(Т0 / Т)3/2,

(1.1)

где μ₀ - подвижность носителей при начальной (комнатной) температуре Т₀.

Аналогичные зависимости имеют место и для других полупроводниковых материалов; отличие заключается только в величинах показателя степени.

Подвижность носителей заряда в примесных полупроводниках обычно уменьшается с повышением концентрации примесей, причем степень влияния концентрации примесей на возрастает при ее увеличении. При очень больших напряженностях электрического поля (больших значениях критической напряженности Екр) подвижность уменьшается по закону

 

μ = μ0√(Eкр/ E),

(1.2)

Здесь μ₀ - подвижность носителей заряда при Е = Е_кр  (для кремния n-типа, например, Е_кр= 2,5 кВ / см).

Подвижность носителей заряда связана с другим параметром полупроводника - коэффициентом диффузии D-соотношением, которое принято называть соотношением Эйнштейна:

D = φ_тμ,

где φ_т = kТ / q - тепловой потенциал, который при комнатной температуре приближенно равен 26 мВ; k - постоянная Больцмана; q - заряд электрона. Коэффициенты D, так же как и подвижности, имеют разные значения для электронов и дырок, причем D_n > D_p.

Еще одним важным параметром полупроводника является время жизни τ. Различают непосредственную рекомбинацию и рекомбинацию через ловушки. Непосредственной рекомбинацией называют переход электрона из зоны проводимости непосредственно в валентную зону, где он занимает вакантный уровень и уничтожает дырку. В некоторых элементах, выполненных на основе арсенида галлия и некоторых других полупроводников, непосредственная рекомбинация может играть важную роль. Однако в таких полупроводниках, как германий и кремний, непосредственная рекомбинация маловероятна.

В большинстве практических случаев главную роль играет рекомбинация через ловушки (рис. 1.5). Ловушками называются глубокие энергетические уровни, расположенные вблизи середины запрещенной зоны.  Ловушки образуются за счет введения особых примесей или наличия дефектов кристаллической решетки полупроводника. Реально всегда существуют и мелкие дефектные уровни (уровни прилипания), которые расположены вблизи дна или потолка запрещенной зоны, но на процесс рекомбинации они практически не влияют.

Рекомбинация через ловушки происходит в два этапа: сначала электрон переходит из зоны проводимости на уровень ловушки, а затем с уровня ловушки в валентную зону. Эти переходы обозначены стрелками на рис. 1.5.

Чем больше в полупроводнике ловушек, тем интенсивнее происходит рекомбинация и соответственно меньше τ. Поэтому малые времена жизни свойственны полкристалла, где дефекты расположены на всех гранях отдельных зерен, и поверхностным слоям монокристаллических полупроводников, где много различных дефектов и посторонних примесей.

В общем  случае движение носителей заряда в полупроводниках обусловлено двумя физическими процессами: диффузией и дрейфом. Диффузией называется направленное перемещение носителей зарядов в следствие неравномерности их концентрации, т.е. перемещение под действием градиента концентрации носителей зарядов. Дрейфом называется направленное перемещение носителей заряда под действием электрического поля.

За время жизни в результате диффузионного движения носители заряда будут проходить некоторое среднее расстояние L, называемое диффузионной длиной. Более строго диффузионная длина определяется как расстояние, на котором концентрация носителей уменьшится в е (~ 2,7) раз. Диффузионную длину можно определить как

 L = √DƮ.

С точки зрения конструирования и эксплуатации элементов полупроводниковой электроники очень важным параметром является удельная проводимость полупроводников.

 

ПРОВОДИМОСТЬ ПОЛУПРОВОДНИКОВ

Поскольку в полупроводниках имеется два типа подвижных носителей заряда, удельная проводимость σ складывается из двух составляющих: электронной и дырочной, т. е.

σ = qnμ_n + qpμ_p.

Поскольку для собственного полупроводника обе составляющие равнозначны, можно записать:

σ_i = qn_i (μ_n + μ_p).

Отметим, что концентрация носителей заряда в собственном полупроводнике при заданной температуре определяется шириной запрещенной зоны. Так, поскольку ε_з, у германия меньше, чем у кремния, n_i, у германия больше (приблизительно на три порядка), чем у кремния. Аналогично для электронного полупроводника запишем:

σ = qnμn .

(1.3)

Формула (1.3) является общей для любого состояния полупроводника n-типа. Если донорная примесь активировалась, то n можно заменить на п_п. Удельная проводимость дырочного полупроводника определяется как

σ = qpμp.

(1.4)

Сравнение (1.3) и (1.4) позволяет сделать важный практический вывод: при равной концентрации примесей электронный полупроводник будет иметь большую удельную проводимость, чем дырочный, поскольку μ_n > μ_p.

Рассмотрим теперь температурную зависимость проводимости полупроводника, например электронного. Так как при температуре абсолютного нуля в полупроводнике отсутствуют свободные носители заряда, то n = 0, следовательно, σ_n = 0. При повышении температуры σ_n будет увеличиваться за счет активации примесных атомов (доноров). В этом случае электроны с донорных уровней (донорной зоны) переходят в зону проводимости (см. рис.1.3), что соответствует возрастанию n в формуле (1.3). Этот рост будет происходить до тех пор, пока не активируется вся примесь. Температура, при которой все атомы примеси уже отдали свои избыточные валентные электроны, принято называть температурой активации t_акт. Эта температура определяется типом примеси и ее концентрацией. В первом приближении можно считать t_акт = -100 ˚С.

Поскольку вся примесь уже активирована, то при дальнейшем повышении температуры концентрация электронов остается практически постоянной. Это соответствует q_n = const в формуле (1.3). Следовательно, теперь изменение проводимости будет определяться лишь изменением подвижности носителей, т.е. σ_n будет изменяться по закону (1.1).

При дальнейшем повышении температуры проводимость резко возрастает за счет интенсивной термогенерации. Здесь температура становится уже достаточной для перевода электронов из валентной зоны в зону проводимости. Поскольку сильно увеличивается как число электронов, так и число дырок (собственная электропроводность преобладает над примесной), то проводимость полупроводника резко возрастает. Температура t_кр, начиная с которой происходит возрастание проводимости, называется критической, или температурой вырождения. Хотя t_кр и зависит от концентрации примесных носителей, определяющим параметром для нее является ширина запрещенной зоны. Чем шире запрещенная зона, тем больше t_кр. Так, если для кремния t_кр ≈ 330 ˚С, то для германия критическая температура будет меньше (~ 100 ˚С).

Рабочий температурный диапазон примесных полупроводников ограничен снизу t_акт, а сверху - t_кр. Абсолютное большинство полупроводниковых устройств электроники и используются в этом диапазоне температур (обычно даже в более узком диапазоне: - 60 ...100 ˚С). Таким образом, основной рабочей областью полупроводника является область, в которой его проводимость уменьшается с ростом температуры.

 

СТРУКТУРА И ОСНОВНЫЕ СВОЙСТВА р-n ПЕРЕХОДА

Прежде всего, рассмотрим два образца полупроводника с электронной и дырочной электропроводностями (рис. 1.6, а). Напомним, что в дырочном полупроводнике присутствуют в равном количестве подвижные положительные дырки и неподвижные отрицательные ионы. На рис. 1.6,а дырки обозначены знаками «плюс», а отрицательные ионы - знаками «минус», заключенными в кружки. Для нашего рисунка концентрация примеси в электронном полупроводнике выбрана в 2 раза меньше, чем в дырочном. Аналогично обозначениям зарядов в дырочном полупроводнике в электронном полупроводнике электроны обозначены знаками «минус», а положительные ионы - со знаками «плюс», заключенными в кружки. Поскольку N_A = 2N_Д, то заряды в дырочном полупроводнике нарисованы в 2 раза чаще, чем в электронном.

Теперь представим, что рассмотренные нами два образца являются просто областями единого кристалла полупроводника (рис. 1.6, б). Тогда по закону диффузии электроны из области n будут перемещаться в область р, а дырки, наоборот, - из области р в область n. Встречаясь на границе р и п областей, дырки и электроны рекомбинируют. Следовательно, в этой пограничной области значительно уменьшается концентрация носителей заряда и обнажаются некомпенсированные заряды неподвижных ионов. Со стороны области обнажаются положительные заряды доноров, а со стороны области р-отрицательные заряды акцепторов. Область некомпенсированных неподвижных зарядов и есть собственно область р-п перехода. Ее часто называют обедненным, истощенным слоем, или i-областью, имея ввиду резко сниженную концентрацию подвижных носителей заряда. Иногда эту область называют запорным слоем электронно-дырочного перехода.

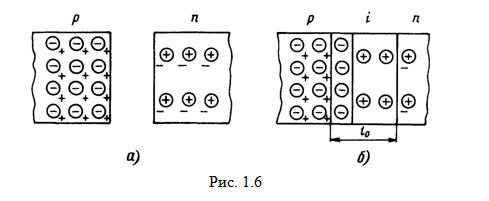
Отметим, что р-п переход в целом должен быть электронейтральным, т.е. отрицательный заряд левой части и положительный заряд правой части должны быть одинаковы. Поскольку в рассматриваемом нами случае N_A = 2N_Д(несимметричный переход), протяженность областей расположения заряд оказывается разной: одну треть i-области занимают акцепторы, а две трети доноры. Таким образом, большая часть обедненной области сосредоточивается в слаболегированном (высокоумном) слое.

В реальных р-п переходах концентрации доноров и акцепторов отличаются на несколько порядков. В таких несимметричных переходах практически весь обедненный слой сосредоточен в слаболегированной части. Ширина обедненного слоя (i-области) в равновесном состоянии l₀ (см. рис. 1.6, б) является важным параметром р-п перехода. Другим, не менее важным параметром равновесного состояния является высота потенциального барьера (контактная разность потенциалов) ∆φ₀. Этот параметр показан на зонной энергетической диаграмме р-п перехода, изображенной на рис. 1.7 (где ε_F - уровень Ферми).

Потенциальный барьер образуется электрическим полем пространственного заряда обедненного слоя. При отсутствии внешнего поля (равновесное состояние) уровень Ферми является общим для всего объема полупроводника и расположен в запрещенной зоне. Поскольку в полупроводнике п-типа уровень Ферми смещен вверх относительно середины запрещенной зоны, а в полупроводнике р-типа вниз, то разрешенные зоны дырочной области должны располагаться на более высоких энергиях, чем разрешенные зоны электронной энергии. Следовательно, в обедненном слое диаграмма энергетических зон искривляется. Заметим, что в i-области уровень Ферми проходит вблизи середины запрещенной зоны.

 

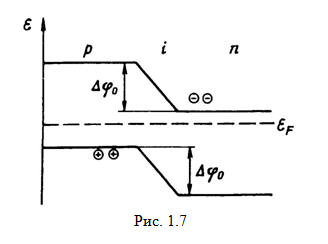
Электрическое поле электронно-дырочного перехода, представляемое на рис. 1.7 потенциальным барьером, препятствует прохождению электронов из области р-типа в область п-типа и дырок в обратном направлении. Более строго: дрейфовые составляющие тока равны диффузионным. С некоторым приближением можно считать, что в равновесном состоянии р-п перехода его внутреннее электрическое поле компенсирует процесс диффузии носителей заряда, в результате чего ток через р-п переход не протекает. Анализируя рис. 1.7, следует помнить, что электроны в зоне проводимости стремятся занять уровни минимальной энергии, а дырки в валентной зоне - максимальной энергии.

Высоту потенциального барьера ∆φ₀ удобно выражать в единицах напряже ния - вольтах. Довольно сильное влияние на величину ∆φ₀ оказывает шири на запрещенной зоны исходного полупроводника: чем больше ε_з, тем больше и ∆φ₀. Так, для большинства р-п переходов из германия ∆φ₀ = 0,35 В. а из кремния - 0,7 В.

Ширина р-п перехода во многом определяется величиной ∆φ₀. Это хорошо видно из общей формулы для l₀ при N_a ›› Nд:

(1.5)

где ε_o, ε_n - диэлектрическая проницаемость вакуума и полупроводника соот ветственно. Величина l₀ обычно составляет десятые доли или единицы микро метра. Из (1.5) следует, что для создания широкого р-п перехода следует ис пользовать малые концентрации примеси, а для создания узкого перехода - большие концентрации. При равных концентрациях примеси l₀ будет больше у р-п перехода с большим ∆φ₀ и, следовательно, с большей ε_з. Таким образом, у кремниевых р-п переходов l₀ обычно больше, чем у германиевых.

Если к р-п переходу подключить внешний источник напряжения, то нару шится условие равновесия и потечет ток. При этом должна измениться высота потенциального барьера и соответственно ширина р-п перехода.

Рассмотрим сначала прямое смещение р-п перехода (рис. 1,8). В этом случае внешнее напряжение U приложено в прямом направлении, т. е. знаком «плюс» к области р-типа. Высота потенциального барьера ∆φ при этом снижается:

∆φ =  ∆φ0 - U

(1.6)

 

Заменив в (1.5) ∆φ₀ на ∆φ и подставив в (1.5), можно убедиться, что и ширина р-п перехода уменьшается при прямом смещении.

Уменьшение высоты потенциального барьера приводит к снижению элек трического поля, препятствующего диффузии носителей заряда. Дырки из области р-типаначинают переходить в область n-типа, а электроны, наоборот, из области р-типа в область n-типа. В каждой области появляются избыточные концентрации неосновных носителей. Процесс нагнетания неосновных носите лей заряда в какую-либо область полупроводника называется инжекцией.

За счет разной концентрации примеси в областях несимметричных р-п переходов концентрации основных носителей тоже будут разные (обычно отличаются на несколько порядков). В рассматриваемом нами случае N_a ›› Nд, следовательно, р_р » р_п. Сильнолегированную дырочную область обозначим как р+ (рис. 1.8). Она имеет относительно малое удельное сопротивление и обычно называется эмиттером. Область n-типа, имеющая относительно большое удельное сопротивление, называется базой.

В несимметричных р-п переходах концентрация инжектированных носите лей из эмиттера в базу всегда гораздо больше, чем в обратном направлении. Параметром, характеризующим степень однонаправленности инжекции, яв­ляется коэффициент инжекции γ. Для рассматриваемого нами перехода можно записать

 

γ = I_р / (I_р + I_n),

 

где Ip, In - токи инжекции дырок и электронов соответственно. В реальных р-п переходах инжекция имеет практически односторонний характер: носители инжектируются в основном из эмиттера в базу (I_р ›› I_n), т. е. γ ≈ 1. Для практиче ских расчетов удобно использовать формулу

 

γ = 1 - ρэ/ρб

(1.7)

 

где ρ_э, ρ_б - удельные сопротивления эмиттера и базы соответственно. Из (1.7) следует, что чем сильнее легирован эмиттер и чем слабее легирована база, тем ближе значение у к единице.

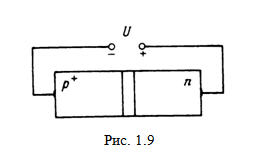
Теперь рассмотрим обратное смещение р-п перехода (рис. 1.9). В этом случае внешнее напряжение U приложено в обратном направлении, т. е. знаком «плюс» к области n-типа. Высота потенциального барьера ∆φ при этом повышается:

 

∆φ =  ∆φ0 + U

(1.8)

 

Подставляя значение ∆φ из (1.8) в формулу (1.5), получаем для неравновес ной ширины р-п перехода l:

 

(1.9)

 

Таким образом, увеличение обратного смещения приводит к расширению р-п перехода. Поскольку несимметричный переход почти полностью расположен в высокоомной базе, то и его расширение происходит в сторону базы. При использовании обратного смещения р-п перехода на практике обычно U » ∆φ. В этом случае (1.9) можно переписать в виде

 

(1.10)

 

При приложении U в обратном направлении концентрации неосновных носителей на границах i-области уменьшаются по сравнению с равновесными значениями. Такой процесс отсоса носителей называется экстракцией.

ВОЛЬТ-АМПЕРНАЯ ХАРАКТЕРИСТИКА р-n ПЕРЕХОДА

В общем виде вольт-амперная характеристика (ВАХ) р-n перехода (рис. 1.10) представляется экспоненциальной зависимостью

 

I = I0 (exp U / φТ  - 1)

(1.11)

 

где I₀ - обратный ток. Этот ток имеет небольшие величины (мкА или нА), но довольно сильно увеличивается при повыше нии температуры. Подробно I₀рассмотрим далее.

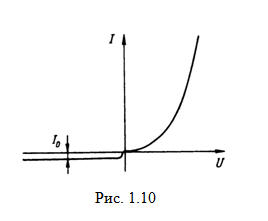Из (1.11) следует, что при прямом смещении (U > 0) ток через р-ппереход возрастает, а при обратном смещении(U < 0) стано вится малым, приближаясь к значению I₀. Поскольку φ_Т = 26 мВ, то при положительных напряжениях U > 0,1В, в формуле (1.11) можно пренебречь единицей по сравнению с экспонентой. Таким образом, р-п переход характеризуется свойством односторонней электропроводности, т. е. хорошо проводит ток в прямом на правлении и плохо в обратном. Следовательно, р-п переход обладает выпрямляющим действием, что позволяет использовать его в качестве выпрямителя переменного тока.

Важным параметром р-п перехода является его дифференциальное сопротивление r_д. Формулу для определенияr_д прямой ветви ВАХ получим из (1.11):

При I ›› I₀ получим окончательно:

rД = φТ / I.

(1.12)

C ростом тока дифференциальное сопротивление р-п перехода быстро падает. При токах порядка единиц и десятков миллиампер r_Д состав ляет десятки и единицы Oм.

При расчете выпрямительных устройств часто пользуются другим параметром р-п перехода - сопротивлением постоянному току R_ст.

Из формулы (1.11) довольно просто получить зависимость R_ст от рабочего тока:

При прямом смещении р-п перехода (при протекании прямого тока) R_ст всегда больше сопротивления r_д.

Поскольку на р-п переходе при больших токах может выделяться достаточно большая мощность, температура перехода при этом может заметно превысить температуру отдельных областей полупроводникового элемента и окружающей среды.

Тепловой баланс в полупроводниковой структуре устанавливается через некоторое время после включения тока и определяется теплопроводностью отдельных частей структуры. С целью повышения максимально допустимой мощности, выделяемой на р-п переходе, прежде всего следует улучшить теплообмен с окружающей средой. Более подробно вопрос теплового режима будет рассмотрен в гл. 3.

При прямом смещении р-п перехода его идеализированная ВАХ согласно (1.11) представляется однородной экспонентой. Однако реальная характеристика имеет несколько более сложную форму: состоит из нескольких участков с разными на клонами. Отличия реальной ВАХ от идеализированной опреде ляются несколькими причинами.

Первая причина обусловлена процессами рекомбинации в i-области р-п перехода. Она имеет место при малых прямых смещениях. В этом случае ∆φ еще велика, следовательно, имеет место малый уровень инжекции, т. е. в i-область из эмиттера и базы попадает малое число носителей заряда. При таком малом положительном смещении ширина перехода lеще довольно большая - объем i-области еще достаточно велик, следователь но, в ней присутствует относительно много ловушек. Таким об разом, за счет большого числа ловушек создаются очень благо приятные условия в i-области для рекомбинации малого числа инжектированных носителей.

В рассмотренном случае ВАХ формируется за счет тока ре комбинации, который тоже имеет экспоненциальную зависи­мость от напряжения, но 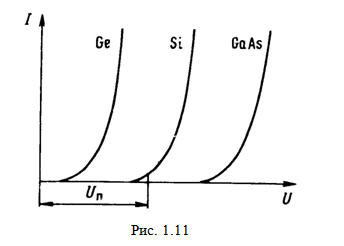более пологую, чем по (1.11). За счет такого пологого начального участка вид прямой ветви реальной ВАХ становится таким, как показано на рис. 1.11. На этом ри сунке представлен параметр U_П, называемый напряжением «пятки». Хотя на сегодняшний день и нет четкого определения для этого параметра, он часто используется для прикидочных расчетов радиоэлектронных устройств. Будем несколько услов но считать, что U_П - это напряжение на р-п переходе, при ко тором I = 0,1 мА. Нетрудно заметить, что чем больше ∆φ₀ и l₀ (чем шире ε₃), тем должно быть больше и U_П. Следовательно, у кремниевых р-п переходов U_П больше, чем у германиевых, и меньше, чем у переходов из арсенида галлия (рис. 1.11). Следует отметить, что в формирование величины U_П определенный вклад вносит и ток I₀.

Другая причина отличия реальной ВАХ от формы (1.11) об условлена падением напряжения на объемном сопротивлении базы. Эта причина проявляется при достаточно больших токах. Заметим, что сопротивление базы r_б в реальных р-п переходах обычно составляет единицы или десятки Ом. Падение напряже ния на этом сопротивлении Ir_б является той поправкой, которую следует ввести в формулу (1.11), чтобы учесть различие между напряжением на самом запорном слое р-п перехода и величиной внешнего напряжения U. С учетом такой поправки получаем

 

I = I0ехр[(U - Irб)/φт].

(1.13)

Падение напряжения на r_б приводит к появлению на ВАХ участка, называемого омическим. При больших токах значение ∆φ₀ становится небольшим, сопротивление обедненного слоя уменьшается и уже оказывается малосущественным, следовательно, в таком случае можно рассматривать р-п переход как простую двухслойную пластину, сопротивление которой приближенно равно сопротивлению ее высокоомного слоя r_б (ρ_э«ρ_б). Необходимо отметить, что учитывать падение напряжения на r_бнеобходимо для значительного, иногда даже основного, рабоче го участка ВАХ р-п перехода.

Еще одна причина отличия реальной ВАХ от идеализирован ной обусловлена модуляцией сопротивления базы при больших уровнях инжекции. Протекание больших токов определяется инжекцией большого числа носителей заряда из эмиттера в базу. В результате присутствия в базе большого числа неосновных носителей заряда ее объемное сопротивление уменьшится. Это обстоятельство делает необходимым учет влияния r_б = f(I) в формуле (1.13) для больших уровней инжекции.

Обратная ветвь ВАХ р-п перехода определяется обратным то ком, который, как отмечалось выше, обычно довольно сильно возрастает при повышении температуры. Не останавливаясь здесь на анализе обратной ветви, рассмотрим влияние темпера туры на прямую ветвь ВАХ р-п перехода. Температурная зависимость прямой ветви ВАХ согласно (1.11) определяется измене ниями I₀ и φ_т . Заметим, что при больших токах необходимо со гласно (1.13) также учитывать изменение r_б. Влияние этих температурно-зависимых параметров на ВАХ приводит к тому, что при малых прямых напряжениях ток возрастает с повышением температуры, а при больших - уменьшается. В принципе су ществует даже точка (область), где величина тока практически не зависит от температуры. Однако эта термостабильная точка редко используется на практике, поскольку имеет место при до статочно больших уровнях инжекции. Для большинства же ре­альных устройств ток в р-п переходе несколько возрастает с по вышением температуры (при постоянном напряжении).

На практике чаще всего принято оценивать влияние темпера туры на ВАХ р-п перехода, определяя изменение напряжения при постоянном токе. Для оценки изменения прямого напряже ния при изменении температуры вводится температурный коэф фициент напряжения (ТКН), характеризующий сдвиг ВАХ по оси напряжений. Обычно ТКН имеет отрицательный знак, что знаменует собой уменьшение напряжения на р-п переходе при постоянном токе с ростом температуры. Отметим, что ТКН зависит от тока и несколько уменьшается с его ростом. Для р-п переходов из кремния ТКН достигает - 3 мВ/град.

ЕМКОСТИ р-n ПЕРЕХОДА

Инерционность р-п перехода во многом определяется его емкостями. Обычно выделяют две основные емкости р-п перехода: диффузионную и барьерную. При прямом смещении р-п перехода из эмиттера в базу инжектируются неос­новные для базы носители заряда. Изменение прямого напряжения на р-п пере­ходе приводит к изменению концентрации этих неравновесных неосновных носителей в базе, т. е. к изменению заряда в ней Q_з. Изменение же заряда, вы званное изменением напряжения, можно рассматривать как действие некото рой емкости. Эта емкость называется диффузионной, поскольку неосновные носители заряда попали в базу за счет диффузии из эмиттера. На практике обычно используется дифференциальная диффузионная емкость С_д

Сд = d Qз / dU = I τ / φт

(1.14)

Из (1.14) следует, что диффузионная емкость будет тем больше, чем больше ток через р-п переход и чем больше время жизни неосновных носителей в базе τ. Емкость С_д во многом определяет быстродействие элементов полупроводнико вой электроники.

При обратном смещении инерционность р-п перехода характеризуется ем­костью, которая называется барьерной (или зарядной). Барьерная емкость Qопределяется изменением пространственного заряда в i-области под действием приложенного напряжения.

Ширина р-п перехода зависит от U по закону (1.10). При изменении l ме няется и число нескомпенсированных ионов в i-области, т. е. меняется ее заряд. По этому р-п переход можно рассматривать как систему из двух проводящих плоскостей, разделенных диэлектриком, т. е. как плоский конденсатор. Вели чину барьерной емкости можно рассчитать по формуле плоского конденсатора:

С = ε₀ε_ПSi / l

Здесь Si - площадь р-п перехода. Подставляя в эту формулу (1.10), получаем

(1.15)

 

Как видно из (1.15), С_б зависит от величины приложенного напряжения, т. е. р-п переход может выполнять функции конденсатора переменной емкости.

В заключение заметим, что, поскольку при прямом смещении р-п переход сужается, барьерная емкость растет. Однако в этом случае С_б оказывается менее существенной, чем С_д.

ОБРАТНЫЙ ТОК р-n ПЕРЕХОДА

Как было отмечено выше, при обратном смещении р-п перехода в нем проте­кает лишь небольшой ток, называемый обратным. Этот ток I₀ и формирует обратную ветвь ВАХ р-п перехода (см. рис. 1.10). В общем случае I₀ состоит из четырех составляющих: теплового тока, тока термогенерации, тока утечки и канального тока.

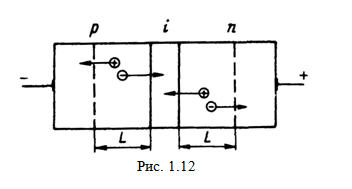
Тепловой ток обусловлен термогенерацией электронно-дырочных пар в об­ластях р- и n-типа, удаленных от i-области не далее чем на диффузионную дли ну (рис. 1.12). Строго говоря, диффузионная длина для эмиттера и базы будет разной, но этот факт не играет принципиальной роли для качественного рас смотрения теплового тока. Электроны и дырки, возникающие в структуре, будут сортироваться электрическим полем: электроны устремляются в n-область, а дырки - в p-область. Следует отметить, что если термогенерации носителей заряда произошла в каком-либо месте структуры, удаленном от i-области более чем на L, то эти носители не смогут уже дойти до i-области - они раньше рекомбинируют и, естественно, не примут участия в образовании теплового тока.

Поскольку тепловой ток обусловлен процессами термогенерации носителей заряда, то он довольно сильно возрастает при увеличении температуры. Обыч но тепловой ток возрастает в 2 раза при увеличении температуры на каждые 10°С. Естественной представляется зависимость теплового тока от ширины запрещенной зоны полупроводника, из которого выполнен р-ппереход. Чем больше ε₃, тем меньше вероятность термогенерации при заданной температуре и, следовательно, меньше тепловой ток. Относительно теплового тока остается заметить, что он является основной составляющей обратного тока у германие вых р-п переходов и слабо зависит от величины приложенного обратного на пряжения.

Другой составляющей обратного тока является ток термогенерации, кото рый обусловлен генерацией носителей заряда в i-области под действием тепла. Этот ток отличается от теплового только местом, где образуются подвижные носители заряда. Величина тока термогенерации пропорциональна объему обедненного слоя, т. е. ширине р-пперехода. Он растет при увеличении l, т. е. пропорционален √U.

Поскольку ток термогенерации, также как и тепловой ток образуется за счет термогенерации носителей заряда, то он, подобно тепловому, возрастает при увеличении температуры. Однако это возрастание происходит более интенсивно. Обычно ток термогенерации возрастает в 3 раза при увеличении температуры на каждые 10°С.

В германиевых р-п переходах ток термогенерации пренебрежимо мал в сравне нии с тепловым, а для переходов из кремния и арсенида галлия может стать заметной частью I₀ при высоких температурах.

Третьей составляющей обратного тока р-п перехода является ток утечки. Для р-п переходов, изготовленных из «достаточно широкозонных полупроводников, поверхностные утечки могут явиться основной составляющей, опреде­ляющей величину тока I₀. Ток утечки обусловлен многими факторами: поверх ностными энергетическими уровнями, молекулярными и ионными пленками, различными загрязнениями и т. д. При повышении напряжения ток утечки возрастает по линейному закону или еще более круто. Влияние же температуры на ток утечки выражено сравнительно слабо. Отметим, что характерной осо бенностью тока утечки является его временная нестабильность. Образование тока утечки, как правило, связано с несовершенством технологии изготовле ния. Примером р-п перехода, у которого ток утечки является основной составляющей обратного тока, является кремниевый переход, выполненный по сплавной технологии.

Четвертой составляющей обратного тока р-п перехода является канальный ток. Он является основной составляющей для кремниевых р-п переходов, вы полненных по планарной технологии. Не вдаваясь здесь в особенности планарной технологии отметим, что при ее использовании поверхность кремниевых р-п переходов покрывается защитной пленкой SiO₂. Это покрытие, с одной стороны, практически устраняет ток поверхностной утечки, но, с другой сторо ны, порождает канальный ток. Канальный ток возникает за счет образования канала (очень тонкого слоя) n-типа в приповерхностной области р-типа, по крытой пленкой SiO₂. Отметим, что канальный ток очень маленький: десятые доли или единицы наноампер.

Заканчивая рассмотрение обратного тока отметим, что, хотя на его величи ну и влияют многие факторы, все же можно считать, что он возрастает при уменьшении ширины запрещенной зоны полупроводника, из которого выпол нен р-ппереход. Так, обратный ток в германиевых р-п переходах обычно на три - четыре порядка выше, чем в кремниевых.

ПРОБОЙ р-n ПЕРЕХОДА

Как отмечалось выше, при рабочих величинах обратных напряжений I₀ неве­лик. Однако при превышении определенного уровня U обратный ток реальногор-п перехода быстро увеличивается, т. е. наступает пробой. Под пробоем р-пперехода понимается явление резкого увеличения обратного тока при до­стижении обратным напряжением определенного критического значения. Все разновидности пробоя р-п перехода можно разделить на две основные группы пробоев: электрические и тепловые. Электрические пробои связаны с увеличе нием напряженности электрического поля в запорном слое р-пперехода, а теп ловые - с увеличением рассеиваемой мощности и соответственно температу ры.

Рассмотрим, прежде всего, основные разновидности электрического пробоя: полевой (зенеровский), лавинный и поверхностный. Вид ВАХ электрического пробоя представлен на рис. 1.13. Основное внешнее отличие разновидностей электрического пробоя проявляется в величинах пробивного напряжения.

В узких р-п переходах при относительно небольших обратных напряжениях (U ≤ 7В) 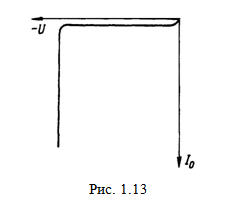обычно возникает полевой пробой. В основе полевого пробоя могут лежать несколько эффектов. Так, под действием большой напряженности элек трического поля становится возможной генерация носителей заряда энергиями меньше ε₃. При малых пробивных напряжениях основным эффектом, опреде ляющим развитие полевого пробоя, становится туннельный. Электрический пробой, возникающий под действием этого эффекта, часто называют туннель­ным.

В относительно широких р-n переходах при обратных напряжениях больше 15 В возникает лавинный пробой, механизм которого заключается в лавинном размножении носителей заряда в сильном электрическом поле под действием ударной ионизации. Электрон и дырка в запорном слое р-пперехода, ускорен ные электрическим полем на длине своего свободного пробега, могут при столкновении с решеткой кристалла разорвать валентную связь. В результате рождается новая пара «электрон-дырка» и процесс повторяется под действием этих новых носителей. Таким образом, сопротивление р-п перехода начинает падать, а ток резко возрастать.

Для того чтобы носители заряда успели приобрести высокую скорость, не обходимую при ударной ионизации, путь и время их разгона должны быть относительно велики. Поэтому лавинный пробой и наблюдается только в ши роких р-ппереходах, т. е. переходах, использующих слаболегированные полу 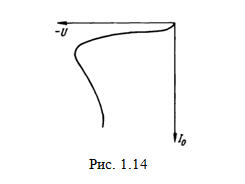проводники.

В области р-п перехода, выступающей на поверхность, обычно имеет место значительное изменение напряженности электрического поля. Поверхностный заряд может привести как к уменьшению, так и к увеличению l. В результате этого на поверхности р-п перехода происходит электрический пробой при на пряжении, меньшем, чем в объеме. Это явление носит название поверхностного пробоя. Большую роль в возникновении поверхностного пробоя играют диэ­лектрические свойства поверхностных покрытий.

В некоторых случаях раньше, чем возникнет электрический пробой, может произойти тепловой. В принципе существует несколько разновидностей и теп лового пробоя - обычно различные локальные пробои. Однако основной интерес представляет тепловой пробой, возникающий за счет большого lо. Этот пробой возникает в тех случаях, когда не обеспечивается необходимый отвод тепла от р-п перехода.

Чаще всего тепловой пробой возникает в мощных германиевых р-п перехо дах, поскольку в них протекает большой обратный ток. Поскольку lо велик, то даже при небольших обратных напряжениях (меньших напряжения электриче­ского пробоя) выделяется большая мощность Р = UI₀. Эта мощность нагревает р-п переход, что вызывает возрастаниеI₀, который, в свою очередь, увеличи вает Р. Такая взаимосвязь приводит к резкому увеличению тока, т. е. к пробоюр-п перехода.

На рис. 1.14 приведена типовая обратная ветвь ВАХ р-п перехода при теп ловом пробое. Такая характеристика имеет участок с отрицательным дифференциальным сопротивлением. Начало этого участка соответствует температуре р-пперехода, близкой к t_кр.

Заметим, что если I₀ вырос благодаря электрическому пробою, то после этого может наступить тепловой пробой. Соответственно на ВАХ после верти кального пробойного участка, свойственного электрическому пробою, может иметь место участок с отрицательным сопротивлением.

Необходимо подчеркнуть, что тепловой пробой является крайне нежела тельным явлением, поскольку он приводит к выходу р-пперехода из строя. Поэтому в тех случаях, когда возможен тепловой пробой, необходимо после довательно с р-п переходом включать токоограничивающее сопротивление.

 

Биполярные транзисторы и тиристоры

Основные определения

Биполярным транзистором называется электропреобразовательный полупроводниковый прибор, имеющий в своей структуре два взаимодействующих p-n-перехода и три внешних вывода, и предназначенный, в частности, для усиления электрических сигналов. Термин “биполярный” подчеркивает тот факт, что принцип работы прибора основан на взаимодействии с электрическим полем частиц, имеющих как положительный, так и отрицательный заряд, - дырок и электронов. В дальнейшем для краткости будем его называть просто - транзистором.

  Структура транзистора, изготовленного по диффузионной технологии, приведена на рис . 3.1. Как видно из рисунка, транзистор имеет три области полупроводника, называемые его электродами, причем две крайние области имеют одинаковый тип проводимости, а средняя область - противоположный. Структура транзистора, приведенная на рис. 3.1, называется n-p-n-структурой. Электроды транзистора имеют внешние выводы, с помощью которых транзистор включается в электрическую схему. Одна из крайних областей транзистора, имеющая наименьшие размеры, называетсяэмиттером (Э). Она предназначена для создания сильного 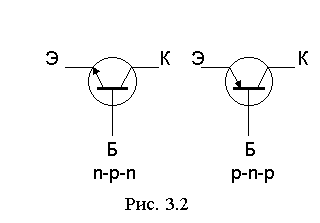потока основных носителей заряда (в данном случае электронов), пронизывающего всю структуру прибора (см. рис 3.1). Поэтому эмиттер характеризуется очень высокой степенью легирования (N_DЭ = 10 ¹⁹ - 10 ²⁰ см ^-3 ). Другая крайняя область транзистора, называемая коллектором (К), предназначена для собирания потока носителей, эмиттируемых эмиттером. Поэтому коллектор имеет наибольшие размеры среди областей транзистора. Легируется коллектор значительно слабее эмиттера (подробнее вопрос о выборе концентрации атомов примеси в коллекторе рассмотрен ниже). Средняя область транзистора называется базой (Б). Она предназначена для управления потоком носителей, движущихся из эмиттера в коллектор. Для уменьшения потерь электронов на рекомбинацию с дырками в базе ее ширина W_Б делается очень маленькой ( W_Б<< L_n), а степень легирования - очень низкой - на 3...4 порядка ниже , чем у эмиттера (N _АБ<<N _DЭ). Между электродами транзистора образуются p-n-переходы. Переход, разделяющий эмиттер и базу, называется эмиттерным переходом (ЭП), а переход, разделяющий базу и коллектор, - коллекторным переходом (КП). С учетом резкой асимметрии эмиттерного перехода (N _DЭ >>N _АБ) он характеризуется односторонней инжекцией: поток электронов, инжектируемых из эмиттера в базу, значительно превосходит встречный поток дырок, инжектируемых из базы в эмиттер.

Режимы работы транзистора

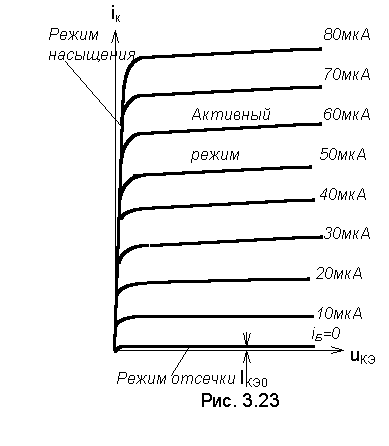
В зависимости от того, в каких состояниях находятся переходы транзистора, различают режимы его работы. Поскольку в транзисторе имеется два перехода (эмиттерный и коллекторный), и каждый из них может находиться в двух состояниях (открытом и закрытом), различают четыре режима работы транзистора. Основным режимом являетсяактивный режим, при котором эмиттерный переход находится в открытом состоянии, а коллекторный - в закрытом. Транзисторы, работающие в активном режиме, используются в усилительных схемах. Помимо активного , выделяют инверсный режим, при котором эмиттерный переход закрыт, а коллекторный - открыт, режим насыщения, при котором оба перехода открыты, и режим отсечки, при котором оба перехода закрыты.

Наряду с транзисторами n-p-n- структуры, существуют транзисторы с симметричной ей p-n-p-структурой, в которых используется поток дырок. Условные обозначения n-p-n- и p-n-p-транзисторов, используемые в электрических схемах, приведены на рис.3.2. Стрелка на выводе эмиттера показывает направление эмиттерного тока в активном режиме. Кружок, обозначающий корпус дискретного транзистора, в изображении бескорпусных транзисторов, входящих в состав интегральных микросхем, не используется. Принцип работы n-p-n- и p-n-p-транзисторов одинаков, а полярности напряжений между их электродами и направления токов в цепях электродов противоположны. В современной электронике наибольшее распространение получили транзисторы n-p-n-структуры, которые, благодаря более высоким значениям подвижности и коэффициента диффузии электронов по сравнению с дырками ( m _n> m _p; D_n>D_p) , обладают большим усилением и меньшей инерционностью, чем транзисторы p-n-p- структуры. Поэтому ниже рассматриваются именно n-p-n- транзисторы.

Схемы включения биполярного транзистора

В большинстве электрических схем транзистор используется в качестве четырехполюсника, то есть устройства, имеющего два входных и два выходных вывода. Очевидно, что, поскольку транзистор имеет только три вывода, для его использования в качестве четырехполюсника необходимо один из выводов транзистора сделать общим для входной и выходной цепей. Соответственно различают три схемы включения транзистора: схемы с общей базой (ОБ), общим эмиттером (ОЭ) и общим коллектором(ОК). На рис. 3.3 показаны полярности напряжений между электродами и направления токов, соответствующие активному режиму в указанных схемах включения транзистора. Следует отметить, что токи транзистора обозначаются одним индексом, соответствующим названию электрода, во внешней цепи которого протекает данный ток, а напряжения между электродами обозначаются двумя индексами, причем вторым указывается индекс, соответствующий названию общего электрода (см. рис. 3.3). В схеме с общей базой (см. рис. 3.3,а)

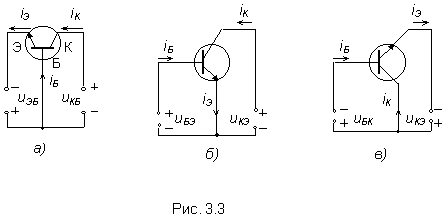
входной цепью является цепь эмиттера, а выходной - цепь коллектора. Схема ОБ наиболее проста для анализа, поскольку в ней каждое из внешних напряжений прикладывается к конкретному переходу: напряжение u_ЭБ прикладывается к эмиттерному переходу, а напряжение u_КБ - к коллекторному. Следует заметить, что падениями напряжений на областях эмиттера, базы и коллектора можно в первом приближении пренебречь, поскольку сопротивления этих областей значительно меньше сопротивлений переходов. Нетрудно убедиться, что приведенные на рисунке полярности напряжений (u_ЭБ<0; u_КБ>0) обеспечивают открытое состояние эмиттерного перехода и закрытое состояние коллекторного перехода, что соответствует активному режиму работы транзистора. 
В схеме с общим эмиттером (см. рис. 3.3,б) входной цепью является цепь базы, а выходной - цепь коллектора. В схеме ОЭ напряжение u_БЭ>0 прикладывается непосредственно к эмиттерному переходу и отпирает его. Напряжение u_КЭ распределяется между обоими переходами:
u_КЭ = u_КБ + u_БЭ . Для того, чтобы коллекторный переход был закрыт, необходимо u_КБ = u_КЭ – u_БЭ > 0 , что обеспечивается при u_КЭ > u_БЭ > 0.
В схеме с общим коллектором (см. рис.3.3,в) входной цепью является цепь базы, а выходной - цепь эмиттера.

Принцип работы биполярного транзистора

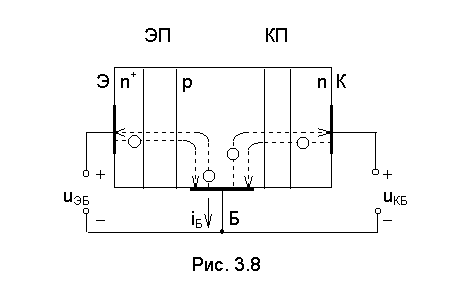
Рассмотрим в первом приближении физические процессы, протекающие в транзисторе в активном режиме, и постараемся оценить, каким образом эти процессы позволяют усиливать электрические сигналы.

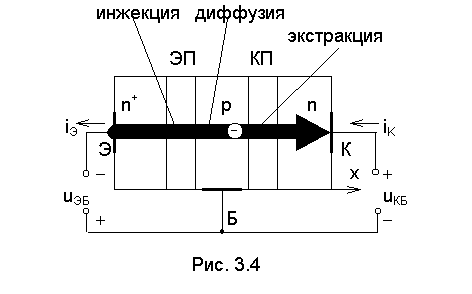Для простоты анализа будем использовать плоскую одномерную модель транзистора, представленную на рис. 3.4. Эта модель предполагает, что p-n- переходы транзистора являются плоскими, и все физические величины в структуре, в частности, концентрации носителей заряда, зависят только от одной продольной координаты x , что соответствует бесконечным поперечным размерам структуры. С учетом того, что в реальной структуре транзистора (см. рис. 3.1) ширина базы значительно меньше поперечных размеров переходов, плоская одномерная модель достаточно хорошо отражает процессы, протекающие в транзисторе. Рассмотрим вначале статическую ситуацию, при которой на переходы транзистора от внешних источников питания подаются постоянные напряжения u_ЭБ и u_КБ - см. рис. 3.4. Заметим, что приведенный на рисунке транзистор включен по схеме с общей базой. Напряжения u_ЭБ <0 и u_КБ >0 обеспечивают открытое состояние эмиттерного перехода и закрытое состояние коллекторного перехода, что соответствует активному режиму работы транзистора. Через открытый эмиттерный переход протекают основные носители заряда. Как уже отмечалось в п. 3.1, из-за резкой асимметрии эмиттерного перехода инжекцию через него можно считать односторонней, то есть достаточно рассматривать только поток электронов, инжектируемых из эмиттера в базу - см. рис. 3.4. Этот поток очень сильно зависит от напряжения на эмиттерном переходе u_ЭБ, экспоненциально возрастая с увеличением ч u_ЭБч . Инжектированные в базу электроны оказываются в ней избыточными (неравновесными) неосновными носителями заряда. Вследствие диффузии они движутся через базу к коллекторному переходу, частично рекомбинируя с основными носителями - дырками. Достигнувшие коллекторного перехода электроны экстрагируются полем закрытого коллекторного перехода в коллектор. В связи с тем, что в коллекторном переходе отсутствует потенциальный барьер для электронов, движущихся из базы в коллектор, этот поток в первом приближении не зависит от напряжения на коллекторном переходе u_КБ. Таким образом, в активном режиме всю структуру транзистора от эмиттера до коллектора пронизывает сквозной поток электронов, создающий во внешних цепях эмиттера и коллектора токи i_Э и i_К , направленные навстречу движению электронов. Важно подчеркнуть, что этот поток электронов и, соответственно, ток коллектора i_К, являющийся выходным током транзистора, очень эффективно управляются входным напряжением u_ЭБ и не зависят от выходного напряжения u_КБ. Эффективное управление выходным током с помощью входного напряжения составляет основу принципа работы биполярного транзистора и позволяет использовать транзистор для усиления электрических сигналов.

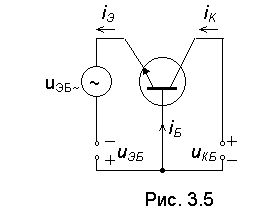  Схема простейшего усилительного каскада на транзисторе, включенном по схеме ОБ, приведена на рис. 3.5. По сравнению со схемой, приведенной на рис. 3.4, в эмиттерную цепь введен источник переменного напряжения u_ЭБ- , а в коллекторную цепь включен нагрузочный резистор R_К. Переменное напряжение u_ЭБ- наряду с напряжением, подаваемым от источника питания, воздействует на сквозной поток электронов, движущихся из эмиттера в коллектор. В результате этого воздействия коллекторный ток приобретает переменную составляющую i_К– , которая благодаря очень высокой эффективности управления может быть значительной даже при очень маленькой величине u_ЭБ- . При протекании тока коллектора через нагрузочный резистор на нем выделяется напряжение, также имеющее переменную составляющую u_КБ- = i_К– R_К. Это выходное переменное напряжение при достаточно большом сопротивлении R_К может значительно превосходить величину входного переменного напряжения u_ЭБ- (u_КБ- >>u_ЭБ- ). Таким образом, транзистор, включенный по схеме ОБ, усиливает электрические сигналы по напряжению. Что касается усиления по току, то рассмотренная схема его не обеспечивает, поскольку входной и выходной токи примерно равны друг другу ( i_Э » i_К ).

3.2. Физические процессы в биполярном транзисторе

Сущность физических процессов, протекающих в транзисторе, таких, как инжекция, экстракция, диффузия, рекомбинация, рассмотрена выше (см. разд. 1 и 2 ). Вместе с тем, в транзисторе проявления этих эффектов имеют определенную специфику, связанную, в первую очередь, с взаимодействием переходов. В этой связи рассмотрим процессы, протекающие в транзисторе применительно к каждому из режимов его работы.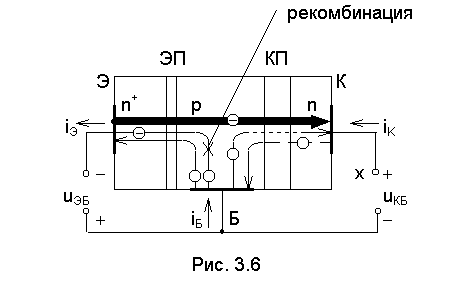

Активному режиму работы транзистора, иногда называемому также нормальным активным режимом, соответствуют открытое состояние эмиттерного перехода и закрытое состояние коллекторного перехода. На рис. 3.6 приведена структура транзистора и показаны потоки носителей заряда в активном режиме. Поскольку основные физические процессы, определяющие протекание в структуре сквозного потока электронов, достаточно подробно описаны в п. 3.1, остановимся лишь на тех моментах, которые были опущены при рассмотрении работы транзистора в первом приближении. Прежде всего, отметим тот факт, что в активном режиме переходы транзистора имеют различную ширину: запертый коллекторный переход значительно шире открытого эмиттерного перехода. На рис. 3.6, наряду с показанным на рис. 3.4 сквозным потоком электронов, показаны и другие потоки носителей, протекающие в структуре в активном режиме. В частности, показан встречный поток дырок, инжектируемых из базы в эмиттер. Два направленных навстречу друг другу потока (электронов и дырок) отражают эффект рекомбинации в базе. Электронный поток создается электронами, которые инжектируются из эмиттера, но не доходят до коллекторного перехода (как электроны, создающие сквозной поток), а рекомбинируют с дырками в базе. Дырочный поток создается дырками, поступающими из внешней цепи в базу для восполнения потери дырок из-за их рекомбинации с электронами. Указанные потоки создают во внешних цепях эмиттера и базы дополнительные составляющие токов. На рис. 3.6 также показаны потоки неосновных носителей заряда, создающие собственный тепловой ток обратносмещенного коллекторного перехода (поток электронов, движущихся из базы в коллектор, и поток дырок, движущихся из коллектора в базу). Каждый из рассмотренных на рис. 3.6 потоков вносит свой вклад в токи, протекающие во внешних цепях эмиттера, коллектора и базы. При этом следует подчеркнуть, что сквозной поток электронов является единственным полезным потоком носителей в транзисторе, поскольку определяет возможность усиления электрических сигналов. Все остальные потоки в усилении сигнала не участвуют, и поэтому являются побочными. Для того, чтобы транзистор имел высокие усилительные свойства, необходимо, чтобы побочные потоки были как можно слабее по сравнению с сильным полезным сквозным потоком. Завершая рассмотрение активного режима, отметим, что основной вклад в ток базы вносит рекомбинационная составляющая. Равная ей рекомбинационная составляющая тока эмиттера определяет его отличие от тока коллектора, создаваемого практически исключительно сквозным потоком электронов. С учетом того, что база транзистора делается очень узкой и слабо легируется, потери электронов на рекомбинацию в базе очень невелики, и i_Б<< i_Э, а i_Э » i_К.
Инверсный режим (инверсный активный режим) работы транзистора аналогичен активному режиму с той лишь разницей, что в этом режиме в открытом состоянии находится коллекторный переход, а в закрытом - эмиттерный переход. В связи с тем, что усилительные свойства транзистора в инверсном режиме оказываются значительно хуже, чем в активном режиме, транзистор в инверсном режиме практически не используется.
В режиме насыщения оба перехода транзистора находятся в открытом состоянии. На рис. 3.7 приведена структура транзистора и показаны потоки носителей, протекающие в режиме насыщения. Как видно из рисунка, в этом режиме и эмиттер, и коллектор инжектируют электроны в базу, в результате чего в структуре протекают два встречных сквозных потока электронов (нормальный и инверсный). От соотношения этих потоков зависит направление токов, протекающих в цепях эмиттера и коллектора. Вследствие двойной инжекции база транзистора очень сильно насыщается избыточными электронами, из-за чего усиливается их рекомбинация с дырками, и рекомбинационный ток базы оказывается значительно выше, чем в активном или инверсном режимах.

 

3.3 Расчет токов биполярного транзистора

Основные допущения идеализированной теории биполярных транзисторов

Для построения идеализированной модели биполярного транзистора будем считать, что его структура разбивается на области пространственного заряда ( обедненные области эмиттерного и коллекторного переходов) и квазинейтральные области эмиттера, базы и коллектора, в которых выполняется условие D n» D p. Кроме того, примем обычные допущения идеализированной теории n-p-перехода:

1.     Области пространственного заряда практически не содержат подвижных носителей заряда и имеют резкие границы с квазинейтральными областями эмиттера, базы и коллектора.

2.     Объемные сопротивления эмиттера, базы и коллектора близки к нулю и внешние напряжения приложены непосредственно к эмиттерному и коллекторному переходам.

3.     На краях областей пространственного заряда (на границах переходов) справедливы граничные уравнения, связывающие концентрации носителей заряда с напряжениями, приложенными к переходам.

4.     В областях эмиттера, базы и коллектора имеет место низкий уровень инжекции неосновных носителей заряда.

Составляющие токов транзистора

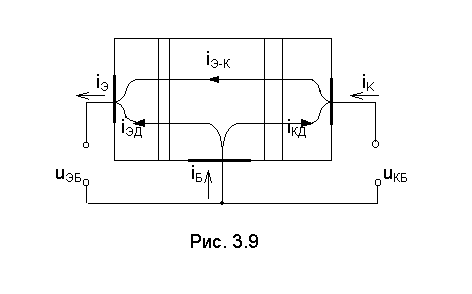Рассмотрим транзистор, включенный по схеме с ОБ (рис 3.9). Во внешних цепях транзистора будут протекать токи i_Э, i_К, i_Б. За положительные направления токов примем указанные стрелками (они совпадают с физическими направлениями токов в активном режиме). Внешние напряжения u_ЭБ и u_КБ , как и ранее, будем отсчитывать от общего электрода (в данном случае - базы). Кроме того , введем напряжения на переходах транзистора u_ЭП - на эмиттерном переходе, u_КП - на коллекторном. Эти напряжения будем считать положительными, если они прямые ( “+” приложен к p- области, а “-” к n-области) и отрицательными, если они обратные.
Для рассматриваемого n-p-n-транзистора в схеме с ОБ
u_ЭП= - u_ЭБ = u_БЭ и u_КП = - u_КБ .
Для p-n-p-транзисторов: u_ЭП= u_ЭБ , u_КП = u_КБ Использование понятий напряжений на переходах позволяет получить одинаковые формулы для n-p-n- и p-n-p-транзисторов.
Как было показано в предыдущей главе, каждый ток содержит различные составляющие; для удобства сгруппируем их следующим образом:

1.     Выделим единственную полезную составляющую, обусловленную переносом электронов из эмиттера в коллектор. Назовем ее током связи i_Э-Кк ( направление тока на рис. 3.9 обратно направлению движения электронов).

2.     Дырочные токи переходов и токи, обусловленные рекомбинацией в базе, объединим в дополнительные токи эмиттерного i _эд и коллекторного i _кд переходов. Эти токи замыкаются каждый через свой переход и не могут передаваться из эмиттера в коллектор. Таким образом, наличие дополнительных токов приводит только к потерям энергии.

Полные токи транзистора могут быть представлены в виде:

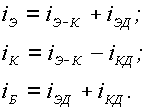 (3.1)
 

Вредные дополнительные токи переходов мало изменяют токи i_Э и i_К ( на 1 - 3 %), однако именно они определяют ток базы.

Перенос электронов из эмиттера в коллектор. Ток связи

Расчет полезной электронной составляющей токов транзистора - тока связи i_Э-К - проведем, пренебрегая малыми дополнительными токами. С физической точки зрения это соответствует отсутствию рекомбинации в базе и переходах транзистора. Электронный поток из эмиттера в коллектор одинаков в любом сечении транзистора, а его величина зависит от процессов в базовой области ( в эмиттере и коллекторе электроны являются основными носителями, их концентрация велика и движение обеспечивается пренебрежимо малыми электрическими полями).

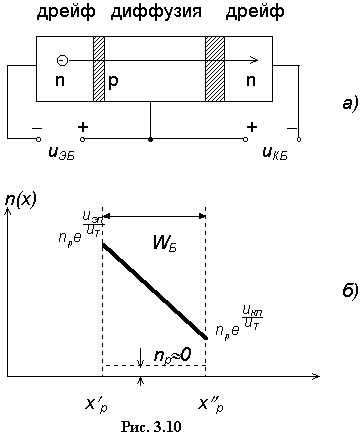Перемещение электронов в базовой области (для нее электроны - неосновные носители) происходит путем диффузии за счет разной концентрации на границах базы с эмиттерным и коллекторным переходами, см. рис. 3.10, ( для определенности будем полагать, что на обоих переходах действуют прямые напряжения u_ЭП >u_КП >0. Естественно, что дальнейшие рассуждения справедливы при произвольных напряжениях на переходах).

Вычисление тока связи будем проводить в произвольном сечении базы в следующей последовательности:

1. Найдем общее решение уравнения диффузии для электронов в базе.
2. Найдем граничные концентрации n(xў_p) и n(xўў_p).
3. Получим распределение n(x) концентрации электронов и определим градиент концентрации 
 

Определим величину диффузионного тока в базовой области, равного току связи. В соответствии с граничным уравнением p-n-перехода получим:

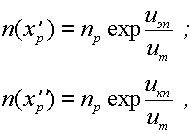 (3.2)
 

где n_p- равновесная концентрация электронов в p-базе. Запишем стационарное уравнение диффузии для электронов:

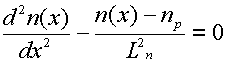 (3.3)
 

Если пренебречь рекомбинацией в базе (это эквивалентно условиюL_n ® Ґ ), то уравнение (3.3) упрощается и приобретает вид:

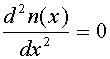 или  (3.4)
 

Таким образом, решением уравнения будет прямая линия, проходящая через точки n(xў _p) и n(x_pўў ). Распределение электронов в p-базе показано на рис 3.10, из которого с учетом (3.2) следует: .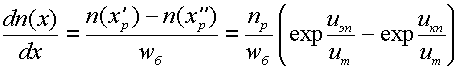
Тогда ток связи может быть рассчитан по формуле: ,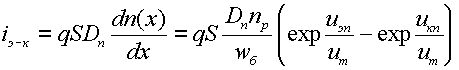
где S - площадь переходов транзистора. Окончательно:

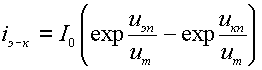(3.5)
 

где 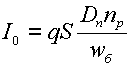 (3.6).

Ток I₀ называется тепловым током транзистора (в зарубежной литературе - током насыщения). Он аналогичен электронной составляющей теплового тока изолированного p-n-перехода.

Часто ток связи представляют в виде разности нормальной i_N и инверсной i_I составляющих.

, (3.7)

где 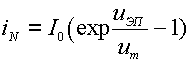 (3.8);

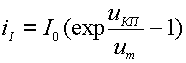(3.9).

Физически i_N - это ток связи при u_КП = 0 , а i_I - ток связи при u_ЭП = 0. Таким образом, ток связи имеет две составляющие, каждая из которых зависит от напряжения на одном из переходов.

Дополнительные токи переходов

 

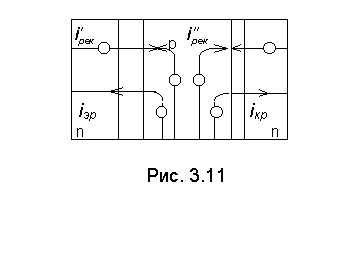
Дополнительные токи переходов складываются из дырочных и рекомбинационных составляющих (см. рис. 3.11). В каждом переходе транзистора, помимо электронных, протекают и дырочные составляющие токов, обусловленные инжекцией дырок - основных носителей заряда в p-базе. Так как концентрация примеси в базе мала N_АБ<<N_DЭ , эти токи в десятки и более раз меньше электронных. Они могут быть рассчитаны по формулам:

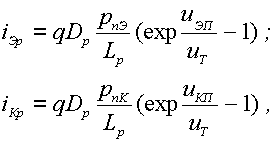 (3.10)

где p_nЭ и p_nК - равновесные концентрации дырок в эмиттере и коллекторе соответственно. Рекомбинационные токи i' _рек и i' ' _рек обусловлены частичной рекомбинацией электронов, диффундирующих из эмиттера в коллектор. Скорость рекомбинации в базе (и рекомбинационные токи) пропорциональны избыточному числу неосновных носителей во всей базовой области (площадь под распределением D n(x) на рис. 3.10. D n(x) = n(x)- n_p ), или

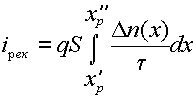 . (3.11)

Учитывая , что распределение D n(x) - линейно, по формуле трапеции получим: 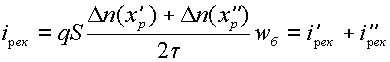, (3.12)

где 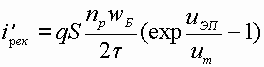; (3.13)

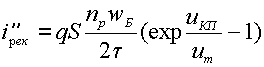 . (3.14)

Ток i' _рек(u_ЭП) определяется рекомбинацией электронов, соответствующих нормальной составляющей тока связи i_N, а i'' _рек(u_КП) - инверсной i_I. Дополнительные токи каждого перехода складываются из рекомбинационных и дырочных составляющих :

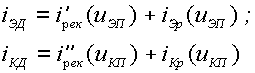 (3.15)

и зависят каждый от напряжения на своем переходе.

Влияние обратного напряжения на коллекторном переходе на токи транзистора. Эффект Эрли

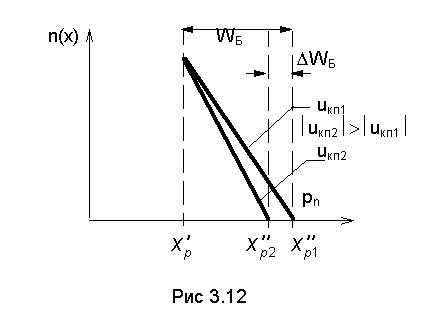В соответствии с формулами 3.5 ...3.8 ток связи перестает зависеть от обратных напряжений при | u_КП| >> u_Т = 26 мВ. Однако реально такая зависимость существует, так как при увеличении обратных напряжений ширина n-p- переходов увеличивается, а ширина базы уменьшается. Зависимость ширины базы от величины обратного напряжения на коллекторе называется эффектом модуляции ширины базы или эффектом Эрли. (Аналогичный эффект в эмиттерном переходе интереса не представляет, так как на эмиттерный переход не подают больших обратных напряжений). На рис 3.12 показаны два распределения n(x) электронов в базе при двух значениях обратного напряжения на коллекторном переходе. Видно, что при u_КП = u_КП2 ширина базы уменьшилась на величину D W_Б. При этом увеличился градиент концентрации электронов

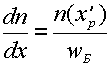 и, следовательно, увеличился и ток связи, являющийся диффузионным. Как следует из рис. 3.12, большему обратному напряжению u_КП2 соответствует больший ток связи i_Э-К а, следовательно, и большие токи i_Э и i_К. Однако данный эффект в сотни раз слабее, чем влияние прямых напряжений на переходах, и часто не учитывается, или учитывается приближенно. Для учета эффекта Эрли уточняют формулу (3.6) теплового тока транзистора I ₀, принимая:

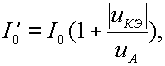 (3.16)

где I₀ - ток, определенный без учета эффекта Эрли по формуле (3.6), u_А - напряжение Эрли - параметр транзистора, характеризующий величину эффекта Эрли. Обычно u_А составляет десятки вольт и более. Физический смысл напряжения Эрли будет рассмотрен позднее в разделе 3.5.

Коэффициенты передачи токов

Полезный эффект в транзисторе создается за счет передачи эмиттерного тока из эмиттера в коллектор. Количественно эффективность этого процесса оценивают с помощью статического коэффициента передачи тока эмиттера a . Введем: 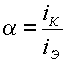 при u_КП = 0. Смысл условия u_КП= 0 заключается в том, что при этом дополнительный ток коллекторного перехода i_КД = 0, и в коллекторной цепи течет только нормальная составляющая i_N полезного электронного тока. Тогда: . .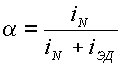
Аналогично можно ввести и инверсный коэффициент передачи тока a _I , или  .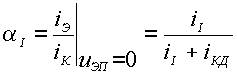
Отсюда следует: a i_N + a i_ЭД = i_N и a _I i_I + a _I i_КД = i_I , тогда

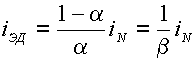, (3.17)

, (3.18)
где:

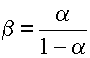 и 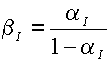 - статические коэффициенты передачи тока базы, прямой и инверсный соответственно. С учетом (3.17) и (3.18) формулы (3.1) удобно представить в виде: ; ;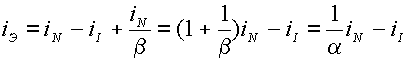

.

 

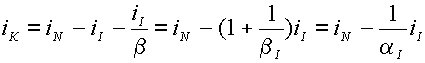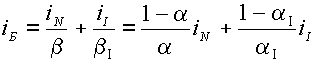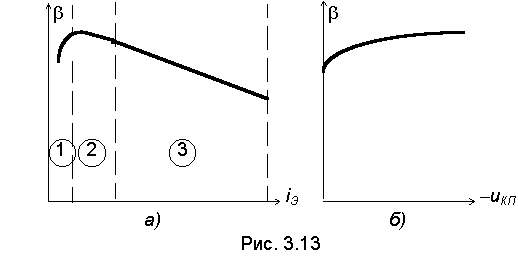В рассматриваемой упрощенной теории коэффициенты a , a _I , b , b _I считаются постоянными, однако опыт показывает, что они изменяются, как при изменении тока связи i_Э-К ( на практике рассматривают зависимость от тока эмиттера i_Э, отличающегося от тока связи на несколько процентов, но легко измеряемого), так и от обратного напряжения на коллекторном переходе u_КП. Типичный вид зависимостей для b показан на рис.3.13 а,б. (Коэффициент a изменяется аналогично, но его изменениями можно пренебречь, так как a » 1. Пример: если a =0,99, то b = a /(1- a ) =99 , а при a=0,98 b =49. Таким образом, изменению a на 1% соответствует изменение b примерно в 2 раза). В области малых токов эмиттера (рис. 3.13а, участок 1) спад b связан с рекомбинацией носителей в самом эмиттерном переходе; в области больших токов (участок 3) уменьшение b связано с увеличением концентрации дырок в базе и возрастанием дырочной составляющей тока эмиттерного перехода. Возрастание b с увеличением обратного напряжения на коллекторе вызвано уменьшением ширины базы и рекомбинационных составляющих токов.

3.4. Нелинейные модели биполярного транзистора

Передаточная модель Эберса-Молла

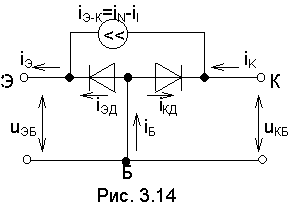
Модель базируется на эквивалентной схеме, приведенной на рис. 3.14. Расчетные формулы, полученные ранее, (см. 3.8, 3.9, 3.17, 3.18) объединим в систему

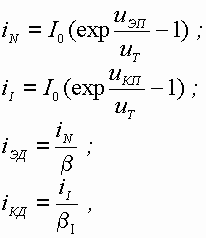:        (3.19)

причем u_ЭП= - u_ЭБ , u_КП = - u_КБ.

Токи во внешних цепях транзистора рассчитываются по формулам:

 (3.20)

В простейшем случае в модели используются три параметра:

• I₀ -тепловой ток транзистора;
• b - прямой коэффициент передачи тока базы;
• b _I - обратный коэффициент передачи тока базы.

Передаточная модель Эберса - Молла может уточняться (влияние объемных сопротивлений, генерационно-рекомбинационных токов переходов, эффект Эрли и т. д.) и поэтому именно она используется в компьютерных программах.

Классическая модель Эберса - Молла

 

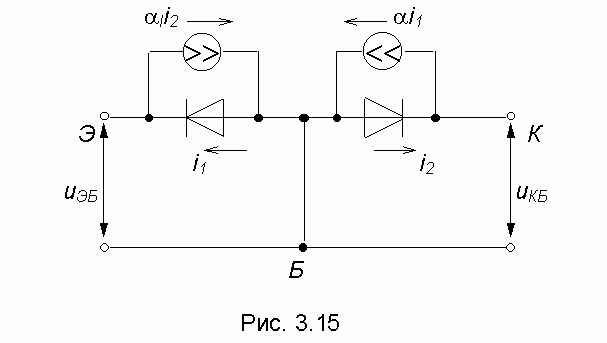
Классическая модель Эберса - Молла базируется на эквивалентной схеме, изображенной на рис. 3.15. От передаточной модели классическая отличается тем, что составляющие токов транзистора сгруппированы иначе. Переходы транзистора представлены изолированными диодами, токи которых i ₁ и i ₂ определяются напряжениями u _эп и u _кп соответственно:
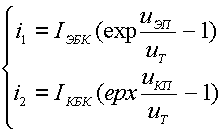, (3.21)

где 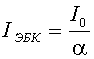 и 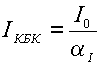. (3.22)

Тепловые токи I_ЭБК и I_КБК имеют следующий смысл:

• I_ЭБК - это тепловой ток эмиттера в схеме с общей базой при u_КП = 0 ( замыкании выводов коллектора и базы).
• I_КБК - тепловой ток коллектора в схеме с ОБ при u_ЭП=0.

Формально тепловые токи соответствуют токам переходов при обратных напряжениях, много больших u _т. Однако реально измеряемые обратные токи переходов транзистора окажутся гораздо больше за счет токов генерации в переходах и токов утечки. (Аналогичная ситуация рассматривалась при анализе p-n-перехода). Поэтому определить значения тепловых токов транзистора можно только по результатам измерений при прямых напряжениях на переходах. Взаимодействие переходов отражено путем введения в эквивалентную схему генераторов тока a i₁ и a _I i₂ .

Соответственно токи в цепях каждого электрода можно рассчитать по формулам: 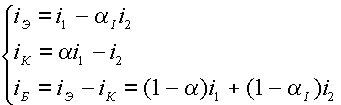 . (3.23)

Классическая модель менее удобна для расчетов, чем передаточная, но широко используется для объяснения работы транзистора.

Модели для активного режима работы транзистора

Рассмотренные выше нелинейные модели транзистора справедливы для любого режима работы. Однако, для наиболее важного активного режима они могут быть существенно упрощены:   Во-первых, можно исключить элементы, описывающие инверсную составляющую тока связи (генератор a _I i₂).   Во-вторых, в качестве одного из аргументов целесообразно рассматривать входной ток транзистора (ток эмиттера в схеме с ОБ и ток базы в схеме ОЭ), так как сопротивление открытого эмиттерного перехода мало, и внешняя цепь по отношению к транзистору в большинстве случаев может рассматриваться как генератор входного тока.

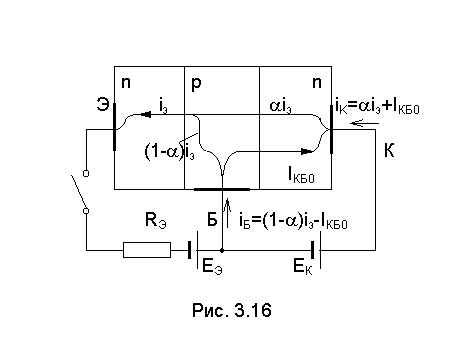  Рассмотрим транзистор в схеме с ОБ, работающий в активном режиме (рис.3.16). Если разорвать цепь эмиттера, то под действием обратного напряжения на коллекторе через коллекторный переход из коллектора в базу будет протекать обратный ток I_КБ0. Его величина приводится в справочных данных транзистора. Подчеркнем, что ток I_КБ0 следует именно измерять, так как аналитически оценить все составляющие обратного тока невозможно (если использовать формулу, связывающую I_КБ0 и I_КБК, получаемую из уравнений Эберса - Молла, то получится очень большая ошибка).

Таким образом, при i_Э =0 , i_К= I_КБ0.

Если теперь замкнуть цепь эмиттера, то появится ток i_Э=E_Э/R_Э (задаваемый внешней цепью). Ток эмиттера будет передаваться в коллектор с коэффициентом a .

В результате получим: i_К =a i_Э+I_КБ0 . (3.24)

Напряжение на эмиттерном переходе можно вычислить с помощью (3.21). Пренебрегая малыми тепловыми токами, получаем:

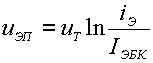. (3.25)

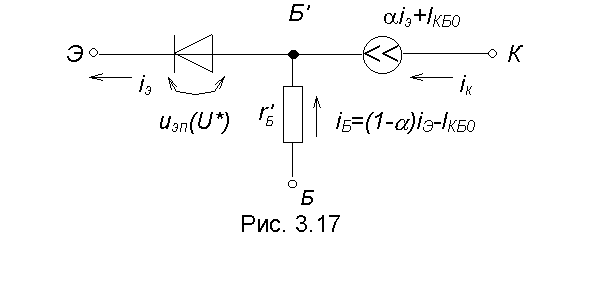Эквивалентная схема транзистора для активного режима приведена на рис. 3.17. В схему добавлено сопротивление тела базы r¢ _Б. Отметим, что в практических расчетах прямое напряжение u_ЭП часто считают не зависящим от тока эмиттера (при изменении тока эмиттера в 10 раз напряжение на эмиттерном переходе изменяется на 60 мВ) и принимают u_ЭП» U*, где U* - пороговое напряжение перехода. Для кремниевых транзисторов U*» 0,6-0,8 В. Током I_КБ0 для кремниевых транзистором пренебрегают.

Для включения с ОЭ (рис.3.18) в качестве входного тока рассматривается ток базы. Учитывая что i_Э= i_К+i_Б, исключим ток i_Э из выражения (3.24) i_К =a ( i_К+i_Б)+I_КБО , тогда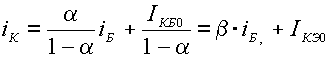 . (3.26)

I_КЭ0 » b I _КБ0 - называется сквозным тепловым током транзистора. Это ток между эмиттером и коллектором при оборванном выводе базы. Для вычисления напряжения на эмиттерном переходе используем (3.25). Считая, что i_Б » (1- a i_Э), получим:

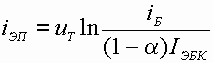 . (3.27)

Эквивалентная схема для включения с ОЭ приведена на рис.3.19.

3.5. Статические характеристики биполярного транзистора

Как уже отмечалось в п. 3.1, транзистор в электрических схемах используется в качестве четырехполюсника, характеризующегося четырьмя величинами: входным и выходным напряжениями и входным и выходным токами ( u_ВХ, u_ВЫХ, i_ВХ, i_ВЫХ). Функциональные зависимости между этими величинами называются статическими характеристиками транзистора, Чтобы установить функциональные связи между указанными величинами, необходимо две из них взять в качестве независимых переменных, а две оставшиеся выразить в виде функций этих независимых переменных. Как правило, применительно к биполярному транзистору в качестве независимых переменных выбирают входной ток и выходное напряжение. В этом случае входное напряжение и выходной ток выражаются следующим образом:

 

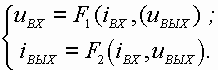
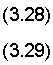
На практике удобнее использовать функции одной переменой. Для перехода к таким функциям необходимо вторую переменную, называемую в этом случае параметром характеристики, поддерживать постоянной. В результате получаются четыре типа характеристик транзистора:

• входная характеристика:

 ; (3.31)

• характеристика обратной передачи ( связи) по напряжению:

 ; (3.32)

• характеристика (прямой) передачи тока, называемая также управляющей или передаточной характеристикой:

 ; (3.33)

• выходная характеристика:

. (3.34)

Статические характеристики транзистора могут задаваться соответствующими аналитическим выражениями, а могут быть представлены графически. Несколько характеристик одного типа, полученные при различных значениях параметра, образуют семейство характеристик. Семейства входных и выходных характеристик транзистора считаются основными и приводятся в справочниках, с их помощью легко могут быть получены два других семейства характеристик. В различных схемах включения транзистора в качестве входных и выходных токов и напряжений выступают токи, протекающие в цепях различных электродов, и напряжения, приложенные между различными электродами. Поэтому конкретный вид статических характеристик зависит от схемы включения транзистора. Рассмотрим статические характеристики транзистора в наиболее распространенных схемах ОБ и ОЭ.

Статические характеристики в схеме ОБ

В схеме с ОБ (см. рис. 3.3,а) входным током является ток эмиттера i_Э, а выходным - ток коллектора i_К, соответственно, входным напряжением является напряжение u_ЭБ, а выходным - напряжение u_КБ.

Входная характеристика в схеме ОБ представляет собой зависимость

.

Однако, реально в справочниках приводится обратная зависимость

.

Семейство входных характеристик кремниевого n-p-n-транзистора приведено на рис. 3.20. Выражение для идеализированной входной характеристики транзистора в активном режиме имеет вид:

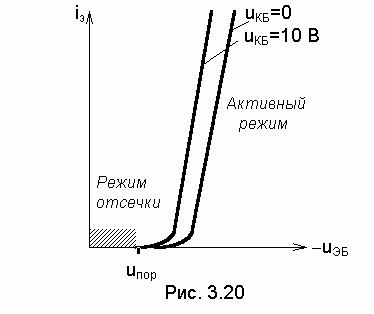Следует отметить, что в выражении (3.35) отсутствует зависимость тока i_Э от напряжения на коллекторном переходе u_КБ. Реально такая зависимость существует и связана она с эффектом Эрли. Как показано в п. 3.3, при увеличении обратного напряжения u_КБ. сужается база транзистора , в результате чего несколько увеличивается ток эмиттера i_Э. Увеличение тока i_Эс ростом u_КБ. отражается небольшим смещением входной характеристики в сторону меньших напряжений | u_ЭБ. | - см. рис. 3.20. Режиму отсечки формально соответствует обратное напряжение u_ЭБ.>0 , хотя реально эмиттерный переход остается закрытым ( i_Э » 0) и при прямых напряжениях | u_ЭБ| меньших порогового напряжения.

Выходная характеристика транзистора в схеме ОБ представляет собой зависимость

.

Семейство выходных характеристик n-p-n-транзистора приведена на рис. 3.21. Выражение дляидеализированной выходной характеристики в активном режиме имеет вид: i_К =a · i_Э+ I_КБ0. (3.36)

В соответствие с этим выражением ток коллектора определяется только током эмиттера и не зависит от напряжения u_КЭ. Реально (см. рис. 3.21) имеет место очень небольшой рост i_К при увеличении обратного напряжения u_КБ, связанный с эффектом Эрли. В активном режиме характеристики практически эквидистантны (расположены на одинаковом расстоянии друг от друга), лишь при очень больших токах эмиттера из-за уменьшения коэффициента передачи тока эмиттера a эта эквидистантность нарушается, и характеристики несколько приближаются друг к другу. При i_Э= 0 в цепи коллектора протекает тепловой ток ( i_К= I_КБ0). В режиме насыщения на коллекторный переход подается прямое напряжение u_КБ, большее порогового значения, открывающее коллекторный переход. В структуре транзистора появляется инверсный сквозной поток электронов, движущийся из коллектора в эмиттер навстречу нормальному сквозному потоку, движущемуся из эмиттера в коллектор. Инверсный поток очень резко увеличивается с ростом Ѕ u_КБ.Ѕ , в результате чего коллекторный ток уменьшается и очень быстро спадает до нуля - см. рис. 3.21.

Статические характеристики в схеме ОЭ

В схеме с общим эмиттером (см. рис. 3.3,б) входным током является ток базы i_Б, а выходным - ток коллектора i_К, соответственно, входным напряжением является напряжение u_БЭ, а выходным - напряжение u_КЭ.

Входная характеристика в схеме ОЭ представляет собой зависимость

.

Однако, реально в справочниках приводится обратная зависимость

.

Семейство входных характеристик кремниевого n-p-n-транзистора приведено на рис. 3.22. Выражение для идеализированной входной характеристики в активном режиме имеет вид:

 , (3.37)

где u_БЭ - прямое напряжение на эмиттерном переходе. Так же, как и в схеме ОБ, входная характеристика имеет вид, характерный для прямой ветви ВАХ p-n-перехода (см. рис. 3.22). однако, входной ток i_Б здесь в ( b + 1) раз меньше, чем в схеме ОБ. Экспоненциальный рост тока базы при увеличении u_БЭ связан с увеличением инжекции электронов в базу и соответствующим усилением их рекомбинации с дырками. В выражении (3.37) отсутствует зависимость тока i_Б от напряжения u_КЭ. Реально эта зависимость имеет место, она связана с эффектом Эрли. Как показано в гл. 3, с ростом обратного напряжения на коллекторном переходе сужается база транзистора, в результате чего уменьшается рекомбинация носителей в базе и, соответственно, уменьшается ток базы. Снижение тока базы с ростом u_КЭ отражается небольшим смещением характеристик в область больших напряжений u_БЭ - см. рис. 3.22.При u_КЭ< u_БЭ открывается коллекторный переход, и транзистор переходит в режим насыщения. В этом режиме вследствие двойной инжекции в базе накапливается очень большой избыточный заряд электронов, их рекомбинация с дырками усиливается, и ток базы резко возрастает - см. рис. 3.22.

Выходная характеристика в схеме ОЭ представляет собой зависимость

.

Семейство выходных характеристик n-p-n-транзистора приведено на рис. 3.23. Выражение для идеализированной выходной характеристики в активном режиме имеет вид:

 . (3.38)

Особенностью выходной характеристики транзистора в схеме с общим эмиттером по сравнению с характеристикой в схеме с общей базой, является то, что она целиком лежит в первом квадранте. Это связано с тем, что в схеме ОЭ напряжение u_КЭ распределяется между обоими переходами, и при u_КЭ< u_БЭ напряжение на коллекторном переходе меняет знак и становится прямым, в результате транзистор переходит в режим насыщения при u_КЭ >0 (cм. рис. 3.23). В режиме насыщения характеристики сливаются в одну линию, то есть ток коллектора не зависит от тока базы. Так же, как и в схеме ОБ, идеализированная характеристика в активном режиме не зависит от напряжения u_КЭ. Реально имеет место заметный рост тока i_К с ростом u_КЭ (см. рис. 3.23), связанный с эффектом Эрли. Этот рост выражен значительно сильнее, чем в схеме ОБ в связи с более резкой зависимостью от напряжения на коллекторном переходе коэффициента передачи тока базы b по сравнению с коэффицентом передачи тока эмиттера a . Также более резкой зависимостью b от тока эмиттера и, соответственно, от тока базы объясняется практическое отсутствие эквидистантности характеристик. При i_Б=0 в цепи коллектора протекает ток i_КЭ0= b i_БЭ0. Увеличение тока в b раз по сравнению со схемой ОБ объясняется тем, что в схеме ОЭ при i_Б=0 и u_КЭ >0 эмиттерный переход оказывается несколько приоткрыт напряжением u_КЭ, и инжектируемые в базу электроны существенно увеличивают ток коллектора.

3.6. Влияние температуры на работу биполярного транзистора

Влияние температуры на работу биполярного транзистора обусловлено тремя физическими факторами: уменьшением потенциальных барьеров в переходах, увеличением тепловых токов переходов и увеличением коэффициентов передачи токов с ростом температуры. Уменьшение потенциального барьера j _К с ростом температуры также, как и в изолированном переходе, (см. раздел 2) приводит к усилению инжекции, в результате чего увеличивается входной ток транзистора. На рис. 3.24 приведены входные характеристики транзистора в схеме с общей базой, полученные при различных температурах (заметим, что входные характеристики в схеме ОЭ при различных температурах выглядят аналогично и отличаются лишь масштабом по оси токов так как i_К >>i_Б. Как видно из рисунка 3.24, увеличение входного тока с ростом температуры эквивалентно смещению характеристики в сторону меньших входных напряжений. Это смещение описывается температурным коэффициентом напряжения 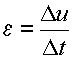, который составляет для кремниевых транзисторов e = - 3 мВ/град. В расчетах транзисторных схем часто используют кусочно-линейную аппроксимацию входных характеристик. На рис. 3.24,б приведены идеализированные аппроксимированные характеристики без учета влияния сопротивления тела базы rў_Б. Как видно из рисунка при rў_Б =0 характеристики проходят вертикально и напряжение на переходе равно пороговому Ѕ - u_ЭБЅ = U*. Изменение этого напряжения с температурой также описывается коэффициентом e .

 

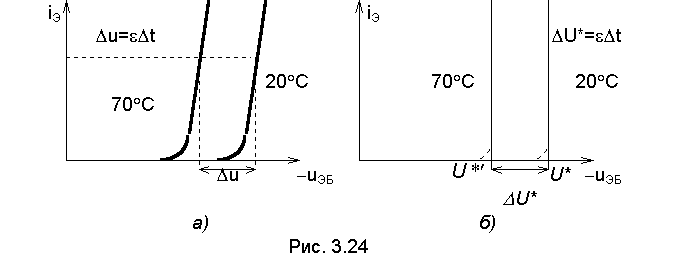
Увеличение тепловых токов переходов с ростом температуры, подробно рассмотренное в разделе 2, описывается приводимыми в справочниках температурными зависимостями токов I_КБ0, I_ЭБ0. Типовые зависимости токов I_КБ0 и I_ЭБ0 от температуры для кремниевого маломощного транзистора приведены на рис. 3.25.

Использование логарифмического масштаба по оси ординат позволило представить экспоненциальную зависимость токов от температуры в линейном виде. Как видно из рисунка, в рабочем интервале температур транзистора (-60 ° ...+ 80 ° C) токи I_КБ0 и I_ЭБ0 могут изменяться на 1...2 порядка. Следует заметить, что отмеченный рост тепловых токов заметно сказывается на выходных характеристиках лишь германиевых транзисторов, что связано с относительно большой величиной самих тепловых токов. В кремниевых транзисторах тепловые токи очень малы, поэтому их изменение с температурой не оказывает заметного влияния на характеристики. Увеличение коэффициента передачи тока эмиттера a и тока базы b с ростом температуры обусловлено ростом времени жизни электронов в базе (см. раздел 1) и соответствующим ослаблением их рекомбинации с дырками. На рис. 3.26 приведены типичные температурные зависимости коэффициентов a и b , нормированных к значениям, полученным при комнатной температуре ( t =20 ° C). Из рисунка видно, что если изменение a с температурой выражено очень слабо (в рабочем интервале температур оно не превышает нескольких процентов), то изменение b может достигать нескольких сотен процентов.

 

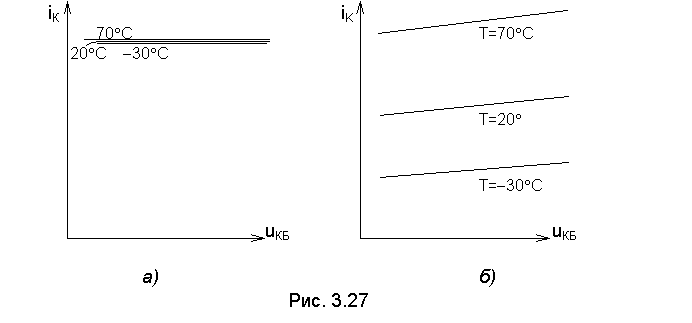
Сказанное выше иллюстрируют приведенные на рис. 3.27 выходные характеристики транзистора в схемах ОБ и ОЭ, полученные при различных температурах. Как видно из рисунка, увеличение температуры приводит к смещению (дрейфу) характеристик в сторону более высоких токов коллектора. При этом в схеме ОБ при фиксированном токе эмиттера D i_К= D ai_Э температурный дрейф характеристик выражен довольно слабо, что объясняется слабой температурной зависимостью коэффициента передачи тока эмиттера a - см. рис 3.26. У характеристик для схемы ОЭ, снимаемых при i_Б =const, в связи с сильной температурной зависимостью коэффициента передачи тока базы b температурный дрейф очень велик - изменение тока коллектора D i_К= D b i_Б может достигать несколько десятков и даже сотен процентов. Температурная нестабильность характеристик транзистора в схеме ОЭ требует специальных мер по стабилизации рабочей точки. На рис. 3.27 приведены три типовые схемы задания режима работы транзистора по постоянному току. В схеме, приведенной на рис 3.27,а внешние элементы задают ток базы

.

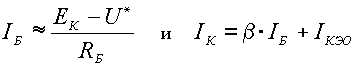Отсюда можно записать выражение для расчета коллекторного тока:

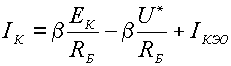 . (3.39)

Оценим изменение тока I_К при изменении температуры на 20 ° С. Будем полагать E_К=10 В, R_Б=100 кОм, b (20 ° С)=100, U*(20 ° С)=0.7В и I_КЭ0(20 ° С)=5мкА, откуда I_К(20 ° С )=100· 10/10 ⁵-100 · 0.7/10 ⁵+5 · 10 ^-6= =9.305 мА. Будем также считать, что изменение b при изменении температуры на 20 ° С составляет 50%, изменение U* определяется коэффициентом e = -2 мВ/град , изменение I_КЭ0 определяется температурой его удвоения T* = 5 ° С. Тогда несложно определить значения b , U* и I_КЭ0 при t ° =40 ° С: b (40 ° С) =1,5·100=150, U*(40 ° С)=0,7-20 ·2 ·10 ^-3=0,66 В и I_КЭ0( 40 ° С)=2 ⁴ ·5 ·10 ^-6=160 мкА. Тогда ток I_К ( 40 ° С)=150·10/10 ⁵-150 ·0,66/10 ⁵+160·10 ^-6=14,17 мА, то есть ток I_К изменился на 52,3 % и основной вклад в это изменение внес коэффициент передачи тока базы b . Расчет показывает, что эта схема обладает низкой температурной стабильностью. В схеме, приведенной на рис. 3.28,б, внешние элементы задают ток эмиттера

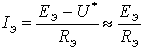 и .

Таким образом, в этой схеме обеспечивается высокая температурная стабильность (как в схеме ОБ), правда достигается она за счет использования дополнительного источника питания. Следует заметить, что указанная схема представляет собой по переменному току - схему ОЭ, а по постоянному току - схему ОБ. Третья схема (см. рис. 3.28,в) занимает промежуточное по термостабильности положение между двумя первыми схемами. В этой схеме фиксируется напряжение u_БЭ и при рациональном выборе R_Б1,R_Б2 и R_Этемпературная стабильность всего в 2 - 3 раза хуже, чем во второй схеме.

 

 

 

 

 

 

 

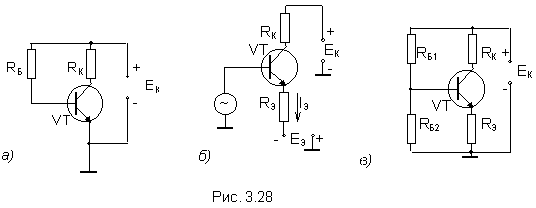
3.7. Пробой биполярного транзистора

Физические причины, вызывающие пробой переходов транзистора, те же, что и в полупроводниковом диоде (см. раздел 2). В то же время пробой переходов в транзисторах имеет определенную специфику, связанную с взаимодействием переходов и проявляющуюся главным образом в схеме с общим эмиттером, где напряжение u_КЭ прикладывается к обоим переходам. В схеме ОБ напряжение лавинного пробоя коллекторного перехода U_{КБ0 проб} близко к напряжению пробоя изолированного перехода. Эмиттерный переход, как правило, работает при прямом смещении и его пробивное напряжение не представляет интереса, однако следует иметь в виду, что из-за сильного легирования эмиттера напряжение пробоя эмиттерного перехода мало - несколько вольт. В схеме ОЭ условия возникновения лавинного пробоя очень сильно зависят от режима базовой цепи. В случае, когда ток базы не ограничен (сопротивление в цепи базы R_Б® 0) пробой коллекторного перехода происходит так же, как и в схеме ОБ, и возникает при том же пробивном напряжении на коллектореU_{КБ0 проб}. При фиксированном токе базы, когда базовая цепь питается от источника тока ( R_Б® Ґ ), проявляется механизм положительной обратной связи, снижающей пробивное напряжения. Его суть состоит в том, что образующиеся в переходе в результате ударной ионизации пары носителей заряда разделяются полем перехода: электроны уходят на коллектор, увеличивая его ток, а дырки скапливаются в базе, увеличивая ее потенциал и снижая потенциальный барьер в эмиттерном переходе. В результате увеличивается инжекция электронов из эмиттера в базу и растет коллекторный ток. Соответственно уменьшается пробивное напряжение. Наиболее сильно накопление дырок в базе происходит при отсутствии базового тока ( i_Б=0), что соответствует разомкнутой цепи базы ( R_Б = Ґ ). В этом режиме пробивное напряжение U_{КЭ0 проб} оказывается в несколько раз ниже, чем в схеме ОБ, и определяется выражением:

U_{КЭ0 проб} = U_{КБ0 проб}  (3.40)

где b= 2...6 - коэффициент, зависящий от материала, из которого изготовлен транзистор. В связи с сильным уменьшением пробивного напряжения запрещается эксплуатация транзистора с разомкнутой базовой цепью.

  На рис 3.29 приведены выходные характеристики транзистора в режиме пробоя. Помимо рассмотренных выше пробивных напряжений U_{КБ0проб} и U_{КЭ0проб} на рисунке показано напряжение U_{КЭRпроб}, соответствующее некоторому конкретному сопротивлению R_Б, включенному в цепь базы и определяющему ее ток. Из рисунка видно, что U_{КЭ0 проб} < U_{КЭR проб}< U_{КБ0проб}. Для увеличения напряжения пробоя коллекторного перехода степень легирования коллектора стараются выбирать достаточно низкой. Так же, как и в полупроводниковом диоде, обратимый лавинный пробой (называемый иногда первичным пробоем) при отсутствии ограничения тока может перейти в тепловой пробой (вторичный пробой), характеризующийся уменьшением напряжения u_КЭ (см. рис. 3.29) и приводящий к выходу транзистора из строя. При этом в транзисторе опасность возникновения теплового пробоя оказывается значительно сильнее, чем в диоде. Это объясняется тем, что за счет инжекции электронов из эмиттера в базу через обратно- смещенный коллекторный переход при больших напряжениях протекает большой обратный ток и, соответственно, велика мощность, рассеиваемая в переходе. Тепловой пробой наступает в том случае, когда рассеиваемая на коллекторе мощность P_К =u_КЭ Ч i_К превышает максимально допустимую рассеиваемую мощность P_{К МАКС}. Гипербола, соответствующая допустимой мощности, показана пунктиром на рис. 3.29. Кроме лавинного и теплового пробоя в транзисторах с очень узкой базой возникает специфический для транзисторной структуры вид пробоя, называемый эффектом смыкания. Он связан с эффектом Эрли и заключается в том, что при очень большом обратном напряжении коллекторный переход, расширяясь, заполняет всю базовую область и смыкается с эмиттерным переходом, что эквивалентно их короткому замыканию.